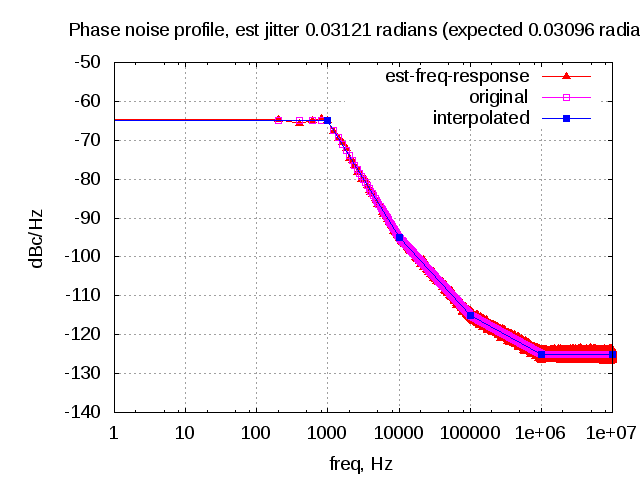
Image Rejection Ratio (IMRR) with transmit IQ gain/phase imbalance

The post on IQ imbalance in transmitter, briefly discussed the effect of amplitude and phase imbalance and also showed that IQ imbalance results in spectrum at the image frequency. In this article, we will quantify the power of the image with respect to the desired tone (also known as IMage Rejection Ratio IMRR) for different values of gain and phase imbalance.

System Model

Consider an IQ modulator having gain of $\alpha$ and $\beta$ on each arm and phase imbalance of $\phi$ as shown in figure below.

Figure : IQ modulator with gain and phase imbalance

The output signal is,

$y(t) = \alpha x_i(t) \cos$2\pi f_c t + \frac{\phi}{2}$ - \beta x_q(t) \sin$2\pi f_c t - \frac{\phi}{2}$$ .

Considering an ideal IQ demodulator multiplying the received signal $y(t)$ with $\cos$2\pi f_c t$$ and $\sin$2\pi f_c t$$ respectively,

$\begin{array}{lll}x'_i(t)&=&\int_0^T\[\alpha x_i(t) \cos$2\pi f_c t + \frac{\phi}{2}$ -\beta x_q(t) \sin$2\pi f_c t - \frac{\phi}{2}$\]\cos$2\pi f_c t $\\&=&\frac{1}{2}\[\alpha x_i(t)\cos$\frac{\phi}{2}$+\beta x_q(t)\sin$\frac{\phi}{2}$\]\end{array}$ .

$\begin{array}{lll}x'_q(t)&=&\int_0^T\[\alpha x_i(t) \cos$2\pi f_c t + \frac{\phi}{2}$ -\beta x_q(t) \sin$2\pi f_c t - \frac{\phi}{2}$\]\[-\sin$2\pi f_c t $\]\\&=&\frac{1}{2}\[\alpha x_i(t)\sin$\frac{\phi}{2}$+\beta x_q(t)\cos$\frac{\phi}{2}$\]\end{array}$ .

Ignoring the common term $\frac{1}{2}$ and writing the base band equivalent form,

${\[\begin{array}x'_i(t)\\x'_q(t)\end{array}\]=\[\begin{array}\alpha \cos$\frac{\phi}{2}$ & \beta \sin$\frac{\phi}{2}$\\\alpha \sin$\frac{\phi}{2}$ & \beta \cos$\frac{\phi}{2}$\end{array}\]\[\begin{array}x_i(t)\\x_q(t)\end{array}\]}$ .

This is the model for transmit IQ imbalance.

Image Rejection Ratio (IMRR) with transmit IQ imbalance

By sending a complex sinusoidal $e^{j\omega t}$ , and by taking ratio of the power of the signal at the image frequency $-\omega$ and desired frequency $+\omega$ , the image rejection ratio can be computed.

Let $x(t) = e^{j\omega t}$ and correspondingly, $x_i(t) = \cos$\omega t$$ and $x_q(t) = \sin$\omega t$$ .

$\begin{array}{lll}x'_i(t)&=&\[\alpha\cos$\frac{\phi}{2}$\cos$\omega t$+\beta \sin$\frac{\phi}{2}$\sin$\omega t$\]\end{array}$

$\begin{array}{lll}x'_q(t)&=&\[\alpha \sin$\frac{\phi}{2}$ \cos$\omega t$ +\beta \cos$\frac{\phi}{2}$ \sin$\omega t$ \]\end{array}$

Finding the $+\omega$ component

To find the $+\omega$ component, multiply the received signal $x'(t)$ with $e^{-j\omega t} = \cos$\omega t$-j\sin$\omega t$$ and integrate over period $T$ .

$\begin{array}{lll}Y_{+w}&=&\int_0^T\[x'_i(t) + jx'_q(t) \]\[\cos$\omega t$ - j\sin$\omega t$\]\\&=&\int_0^T\[x'_i(t)\cos$\omega t$ + x'_q(t)\sin$\omega t$ \]+ j\[-x'_i(t)\sin$\omega t$+x'_q(t)\cos$\omega t$\]\\&=&\frac{1}{2}$\[\alpha\cos\(\frac{\phi}{2}$+\beta\cos$\frac{\phi}{2}$\] + j\[-\beta\sin$\frac{\phi}{2}$+\alpha\sin$\frac{\phi}{2}$\]\)\end{array}$

The power of the $+\omega$ component is,

$\begin{array}{lllll}P_{+w}&=&\|Y_{+w}\|^2&=&\|\frac{1}{2}$\[\alpha\cos\(\frac{\phi}{2}$+\beta\cos$\frac{\phi}{2}$\] + j\[-\beta\sin$\frac{\phi}{2}$+\alpha\sin$\frac{\phi}{2}$\]\)\|^2\\&&&=&\frac{1}{4}\[\alpha^2\cos^2$\frac{\phi}{2}$+\beta^2\cos^2$\frac{\phi}{2}$+2\alpha\beta\cos^2$\frac{\phi}{2}$+\alpha^2\sin^2$\frac{\phi}{2}$+\beta^2\sin^2$\frac{\phi}{2}$-2\alpha\beta\sin^2$\frac{\phi}{2}$\]\\&&&=&\frac{1}{4}\[\alpha^2 + \beta^2+2\alpha\beta\cos$\phi$\]\end{array}$

Finding the $-\omega$ component

To find the $-\omega$ component, multiply the received signal $x'(t)$ with $e^{j\omega t} = \cos$\omega t$+j\sin$\omega t$$ and integrate over period $T$ .

$\begin{array}{lll}Y_{+w}&=&\int_0^T\[x'_i(t) + jx'_q(t) \]\[\cos$\omega t$ + j\sin$\omega t$\]\\&=&\int_0^T\[x'_i(t)\cos$\omega t$ - x'_q(t)\sin$\omega t$ \]+ j\[x'_i(t)\sin$\omega t$+x'_q(t)\cos$\omega t$\]\\&=&\frac{1}{2}$\[\alpha\cos\(\frac{\phi}{2}$-\beta\cos$\frac{\phi}{2}$\] + j\[\beta\sin$\frac{\phi}{2}$+\alpha\sin$\frac{\phi}{2}$\]\)\end{array}$

$\begin{array}{lllll}P_{-w}&=&\|Y_{-w}\|^2&=&\|\frac{1}{2}$\[\alpha\cos\(\frac{\phi}{2}$-\beta\cos$\frac{\phi}{2}$\] + j\[\beta\sin$\frac{\phi}{2}$+\alpha\sin$\frac{\phi}{2}$\]\)\|^2\\&&&=&\frac{1}{4}\[\alpha^2\cos^2$\frac{\phi}{2}$+\beta^2\cos^2$\frac{\phi}{2}$-2\alpha\beta\cos^2$\frac{\phi}{2}$+\alpha^2\sin^2$\frac{\phi}{2}$+\beta^2\sin^2$\frac{\phi}{2}$+2\alpha\beta\sin^2$\frac{\phi}{2}$\]\\&&&=&\frac{1}{4}\[\alpha^2 + \beta^2-2\alpha\beta\cos$\phi$\]\end{array}$

The Image Rejection Ratio (IMRR) is

$\begin{array}{lll}IMRR & = & \frac{P_{-w}}{P_{+w}}\\&=&\frac{\alpha^2 + \beta^2-2\alpha\beta\cos$\phi$}{\alpha^2 + \beta^2+2\alpha\beta\cos$\phi$}\end{array}$ .

Substituting $\alpha$ and $\beta$ with variable $\gamma = \frac{\alpha}{\beta}$ and $\epsilon = \gamma-1$ , the equation simplifies to,

$\begin{array}{lll}IMRR & &=&\frac{\gamma^2 +1-2\gamma\cos$\phi$}{\gamma^2 +1+2\gamma\cos$\phi$}\end{array}$ .

A useful approximation to IMRR

When there is no phase imbalance i.e $\phi=0$ , the equation reduces to,

$\begin{array}{lll}IMRR_{(\phi=0)}&=&\frac{\gamma^2 +1-2\gamma}{\gamma^2 +1+2\gamma}=\frac{(\gamma-1)^2}{(\gamma+1)^2}\\&=&\frac{\epsilon^2}{(\epsilon+2)^2}=\frac{\epsilon^2}{\epsilon^2+4\epsilon+4}\\&\simeq &\frac{\epsilon^2}{4}\end{array}$ .

When there is no gain imbalance i.e $\gamma=1$ , the equation reduces to,

$\begin{array}{lll}IMRR_{(\gamma=1)}&=&\frac{2$1-\cos(\phi)$}{2$1+\cos(\phi)$}\\&=&\tan^2$\frac{\phi}{2}$\\&\simeq &\frac{\phi^2}{4}\end{array}$ .

As these two are independent, they can be added to give an approximate value of Image Rejection Ratio.

Summarizing, the Image Rejection Ratio for a given value of gain imbalance $\gamma, \mbox{ } $\epsilon = \gamma-1$$ and phase imbalance $\phi$ is,

${\begin{array}{lll}IMRR & &=&\frac{\gamma^2 +1-2\gamma\cos$\phi$}{\gamma^2 +1+2\gamma\cos$\phi$}&\simeq&\frac{\epsilon^2+\phi^2}{4}\end{array}}$ .

Simulation Results

Simple Matlab/Octave code plotting the simulated and theoretical values of Image Rejection for different values of gain and phase imbalance.

clear; close all

N  = 64;
fm = 2;
gammadB_v = [-3:.1:3];
phiDeg_v  = [-6:.2:6];
[tt gammadB_zeroIdx ] = min(abs((gammadB_v-0)));
[tt phiDeg_zeroIdx  ] = min(abs((phiDeg_v-0)));

for (ii = 1:length(gammadB_v))
   for (jj = 1:length(phiDeg_v))
      gammadB    = gammadB_v(ii); 
      phiDeg     = phiDeg_v(jj);
      gammaLin   = 10^(gammadB/20); 
      phiRad     = phiDeg*pi/180;
      epsilonLin = gammaLin -1 ;

      % transmitted signal
      xt        = exp(j*2*pi*fm*[0:N-1]/N);
      % received signal with IQ imbalance
      xht_re    = gammaLin*cos(phiRad/2)*real(xt) + sin(phiRad/2)*imag(xt);
      xht_im    = gammaLin*sin(phiRad/2)*real(xt) + cos(phiRad/2)*imag(xt);
      xht       = xht_re + j*xht_im; 

      % taking ifft() to find the +fm and -fm components
      yF        = fft(xht,N);
      y_pfm     = yF(fm+1);
      y_nfm     = yF(N-fm+1);

      est_imrr_lin    = (abs(y_nfm)./abs(y_pfm))^2;
      theory_imrr_lin = (gammaLin^2 + 1  - 2*gammaLin*cos(phiRad))./(gammaLin^2 + 1  + 2*gammaLin*cos(phiRad));
      approx_imrr_lin = (epsilonLin^2 + phiRad^2)/4;

      est_imrr_dB(ii,jj)    = 10*log10(est_imrr_lin);
      theory_imrr_dB(ii,jj) = 10*log10(theory_imrr_lin);
      approx_imrr_dB(ii,jj) = 10*log10(approx_imrr_lin);
   end
end

figure
plot(gammadB_v,theory_imrr_dB(:,phiDeg_zeroIdx),'bs-'); hold on
plot(gammadB_v,est_imrr_dB(:,phiDeg_zeroIdx),'md-');
plot(gammadB_v,approx_imrr_dB(:,phiDeg_zeroIdx),'gx-');
xlabel('gain imbalance, dB'); ylabel('image rejection, dB'); grid on;
legend('theory','estimated','approx')
title('Image Rejection Ratio with gain imbalance alone');
axis([-3 3 -50 -10]);

figure
plot(phiDeg_v,theory_imrr_dB(gammadB_zeroIdx,:),'bs-'); hold on
plot(phiDeg_v,est_imrr_dB(gammadB_zeroIdx,:),'md-');
plot(phiDeg_v,approx_imrr_dB(gammadB_zeroIdx,:),'gx-');
xlabel('phase imbalance, degree'); ylabel('image rejection, dB'); grid on;
legend('theory','estimated','approx')
title('Image Rejection Ratio with phase imbalance alone');
axis([-6 6 -50 -20]);

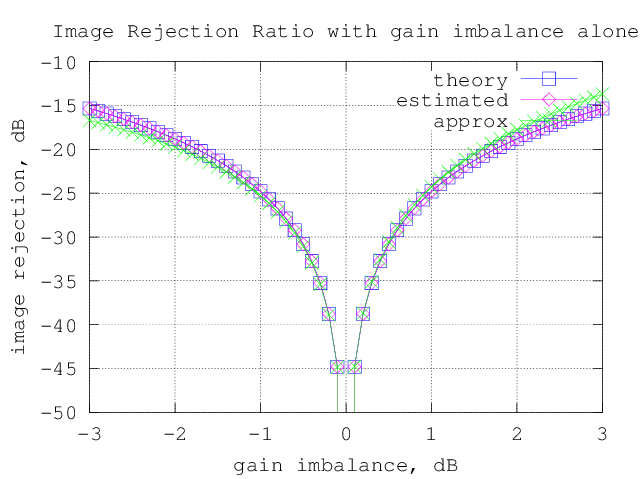
Figure : Image Rejection Ratio (IMRR) with gain imbalance alone

Figure : Image Rejection Ratio (IMRR) with phase imbalance alone

Observations

1) The approximate expression holds good for reasonable values of gain and phase imbalance.

2) As a rule of thumb, the following numbers are useful :

– For 1 degree of phase imbalance, the Image Rejection Ratio (IMRR) is around -41dB

– For 1dB of gain imbalance, the Image Rejection Ratio (IMRR) is around -25dB

References

[1] Cavers, J.K.; Liao, M.W.; , “Adaptive compensation for imbalance and offset losses in direct conversion transceivers,” Vehicular Technology, IEEE Transactions on , vol.42, no.4, pp.581-588, Nov 1993 doi: 10.1109/25.260752

[2] Table of trignometric identities http://www.sosmath.com/trig/Trig5/trig5/trig5.html

Migrated to Amazon EC2 instance (from shared hosting)

GATE-2012 ECE Q28 (electromagnetics)