Question 39 on communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.
Q39. The signal }) as shown is applied both to a phase modulator (with
as shown is applied both to a phase modulator (with  as the phase constant) and a frequency modulator (with
as the phase constant) and a frequency modulator (with  as the frequency constant) having the same carrier frequency.
as the frequency constant) having the same carrier frequency.
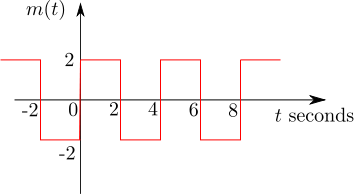
The ratio  }) for the same maximum phase deviation is,
for the same maximum phase deviation is,
(A) 
(B) 
(C) 
(D) 

Solution
To answer this question, let us understand basics of Frequency modulation and Phase modulation. Am referring to the discussion in Section 10 of Electronic Communication, 4th Edition, Dennis Roddy, John Coolen (buy from Amazon.com, buy from Flipkart.com).
Frequency Modulation
In frequency modulation, the modulation signal will cause a change in the instantaneous carrier frequency and is related as
where
is the frequency deviation constant expressed in hertz/volt (Hz/V) and
is the carrier frequency in Hz.
The angular velocity radians per second.
Since the rate of change of phase is the angular velocity,
and so, the instantaneous phase is
.
The frequency modulated carrier signal is
Phase modulation
In phase modulation, the modulation signal will cause a change in phase and the instantaneous phase is
where
is the phase deviation constant expressed in radians/volt and
is the carrier frequency in radians per second.
The phase modulated carrier signal is
.
Now, applying the above equations to solve the problem :
In frequency modulation case, the maximum phase deviation happens when the term hits the maximum.
In phase modulation case, the maximum phase deviation happens when the term hits the maximum.
.
The ratio is,
and so,
Based on the above, the right choice is (B)
References
[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf
[2] Electronic Communication, 4th Edition, Dennis Roddy, John Coolen (buy from Amazon.com, buy from Flipkart.com).




Though the answer seems to right..mathematically there is a glitch i believe..why have integrated from 0 to t when the signal exists from “- infinity” ?..you should have integrated from “- infinity” to “t” right ?..basically i am just saying proof is not complete..though you will get the same answer when you make it complete :)..
Sorry for being so critical on math rather than engineering!! 🙂
@Raghava: Yes, this point briefly crossed my mind when writing up – however, since we are only concerned with the max() value, later forgot about it. Doing a re-read, seems the integral can be changed from -infinity to t with out affecting any other description.
It feels nice to have you cross-checking the accuracy of the answers. Thanks much ! 🙂