Question 3 on Communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.
Q3. In a baseband communications link, frequencies upto 3500Hz are used for signalling. Using a raised cosine pulse with 75% excess bandwidth and for no inter-symbol interference, the maximum possible signaling rate in symbols per second is,
(A) 1750
(B) 2625
(C) 4000
(D) 5250

Solution
To answer this question, am using contents from Section 5.1 of Digital Communication, third edition, John R. Barry, Edward A. Lee, David G. Messerschmitt (buy from Amazon.com, buy from Flipkart.com).
Let us first try to understand the minimum bandwidth required to transmit the signal at symbol rate
with no inter symbol interference (ISI).
The transmitted signal is,
,
where
is the
transmitted data symbols,
is the symbol rate and
is the pulse shape.
The sampled signal is,
.
Decomposing the above equation into two parts,
.
The first term is the desired signal and the second term contributes to inter symbol interference.
To ensure that there is no intersymbol interference, the sampled pulse shape should be
.
Taking Fourier transform, this translates to the following criterion
.
Note : For convenience, take
.
Note :
The proof for this is discussed in bit more detail in Section 9.2 of Digital Communications, 4th edition John G. Proakis (buy from Amazon.com, buy from Flipkart.com)
Let us assume that pulse shape has a bandwidth
. There are three cases to check
i) When :
In this case, the plot of will have non-overlapping replicas of the spectrum
separated by
and there is no choice to meet the
criterion.
ii) When :
There exists one candidate meeting the criterion,
.
The corresponding pulse shape is
.
Alternately, this can be stated as – for a given single sided bandwidth , the maximum symbol rate which can be achieved for ISI free transmission is
. To meet this, the pulse shape
has to be a sinc function. Typically usage of the sinc function is not preferred as its tails decay very slowly and a small timing error in the demodulator will result in an infinite series of inter symbol interference components.
iii) When
In this case consists of overlapping spectrum of
separated by
and there exists multiple choices meeting the
criterion.
A commonly used pulse shaping filter satisfying the criterion while having a faster decay is the raised cosine filters having the following equation,
.
The frequency response is,
.
With a raised cosine pulse shape, the bandwidth is larger than the minimum required pulse shape and is related as,
.
Then term is called the excess bandwidth factor. For example,
translates to 75% excess bandwidth
translates to 100% excess bandwidth
, the raised cosine pulse shape reduces to sinc pulse shape.
In our question,
and
and the goal is to find the maximum possible symbol rate
.
Substituting for ,
and solving for
,
.
Matlab example
% script for plotting the time and frequency response of raised cosine pulse shape % filter with % a) alpha = 0 (sinc pulse) % b) alpha = 3/4 % clear all; close all; fs = 10; % defining the sinc filter sincNum = sin(pi*[-fs:1/fs:fs]); % numerator of the sinc function sincDen = (pi*[-fs:1/fs:fs]); % denominator of the sinc function sincDenZero = find(abs(sincDen) < 10^-10); sincOp = sincNum./sincDen; sincOp(sincDenZero) = 1; % sin(pix/(pix) =1 for x =0 alpha = 0; cosNum = cos(alpha*pi*[-fs:1/fs:fs]); cosDen = (1-(2*alpha*[-fs:1/fs:fs]).^2); cosDenZero = find(abs(cosDen); cosOp(cosDenZero) = pi/4; gt_alpha0 = sincOp.*cosOp; GF_alpha0 = (1/fs)*fft(gt_alpha0,1024); alpha = 0.75; cosNum = cos(alpha*pi*[-fs:1/fs:fs]); cosDen = (1-(2*alpha*[-fs:1/fs:fs]).^2); cosDenZero = find(abs(cosDen); cosOp(cosDenZero) = pi/4; gt_alpha0 = sincOp.*cosOp; GF_alpha0 = (1/fs)*fft(gt_alpha0,1024); alpha = 0.75; cosNum = cos(alpha*pi*[-fs:1/fs:fs]); cosDen = (1-(2*alpha*[-fs:1/fs:fs]).^2); cosDenZero = find(abs(cosDen) cosOp(cosDenZero) = pi/4; gt_alpha_p75 = sincOp.*cosOp; GF_alpha_p75 = (1/fs)*fft(gt_alpha_p75,1024);
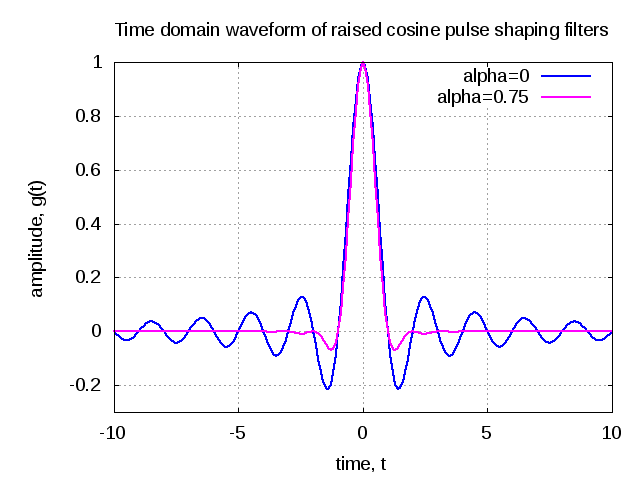
Figure : Time domain plot
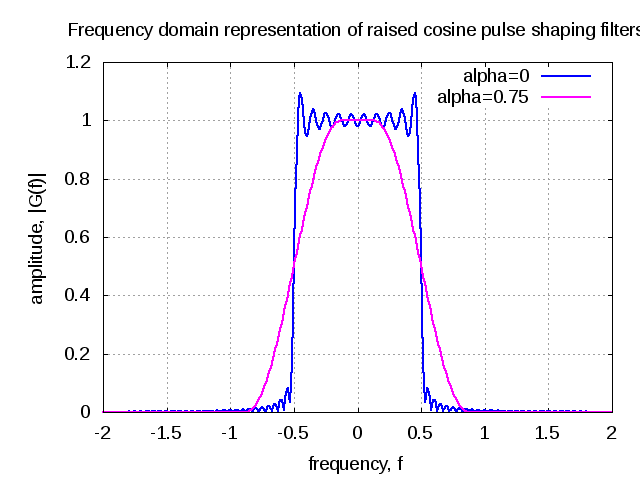
Figure : Frequency domain plot
Based on the above, the right choice is (C) 4000 symbols per second.
References
[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf
[2] Digital Communication, Third edition, John R. Barry, Edward A. Lee, David G. Messerschmitt (buy from Amazon.com, buy from Flipkart.com)
[3] Digital Communications, Fourth edition John G. Proakis (buy from Amazon.com, buy from Flipkart.com)



