Question 36 on math from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.
Q36. A fair coin is tossed till a head appears for the first time. The probability that the number of required tosses is odd, is
(A) 1/3
(B) 1/2
(C) 2/3
(D) 3/4

Solution
Let us start by finding the sample space. The possible sample space with odd number of tosses till a head appears for the first time is,
Given that the coin is fair,
.
The total probability is,
Using Taylor series,
.
Substituting,
Matlab/Octave example
Felt it would be nice to get similar results using a simple simulation model
% Script to find the probability that odd number of tosses % are required to get a head for the first time clear all; close all; N = 5*10^5; % HEAD = 0, TAIL = 1; % definfing the pattern corresponding to odd tosses % till the first head - limiting to max of 21 tosses % converted to integer (for easy comparison) pattern_v = [ ... sum(2.^0 .* [0 ]); ... % H sum(2.^(2:-1:0) .* [1 1 0 ]); ... % TTH sum(2.^(4:-1:0) .* [1 1 1 1 0 ]); ... % TTTTH sum(2.^(6:-1:0) .* [1 1 1 1 1 1 0 ]); ... % TTTTTTH sum(2.^(8:-1:0) .* [1 1 1 1 1 1 1 1 0 ]); ... % TTTTTTTTH ... sum(2.^(10:-1:0) .* [1 1 1 1 1 1 1 1 1 1 0 ]); ... sum(2.^(12:-1:0) .* [1 1 1 1 1 1 1 1 1 1 1 1 0 ]); ... sum(2.^(14:-1:0) .* [1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 ]); ... sum(2.^(16:-1:0) .* [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 ]); ... sum(2.^(18:-1:0) .* [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 ]); ... sum(2.^(20:-1:0) .* [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 ]); ... ]; % finding the probability for each event in the sample space event_v = [1:2:21]; for ii=1:length(event_v) kk = event_v(ii); x = rand(N,kk)>0.5; xVal = sum((ones(N,1)*[2.^([kk-1:-1:0])]).*x,2); matchCnt(ii) = size(find(xVal==pattern_v(ii)),1); end totalProb = sum(matchCnt./N)
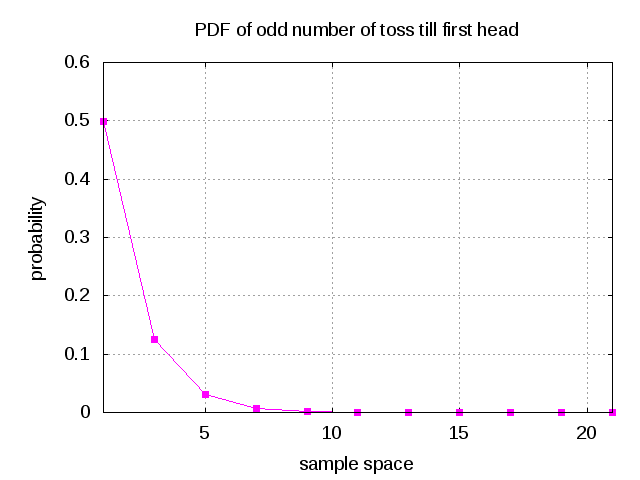
Figure : Probability of odd number of tosses till first head
Based on the above, the right choice is (C) 2/3.
References
[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf
[2] Wiki entry on Taylor series http://en.wikipedia.org/wiki/Taylor_series



