Modeling phase noise (frequency domain approach)

In typical wireless system simulations, there is  a need to model the phase noise profile of the local oscillator. For eg, the phase noise profile of the oscillator can be of the shape described in the post on Phase Noise Power Spectral Density to Jitter. While looking around for example Matlab code, found two references [1, 2] which uses the approach of defining the phase noise profile in frequency domain, and then using ifft() to convert to the time domain samples. This post gives a brief overview of the modeling and provides an example Matlab/Octave code.

Modeling

a) Assume a system with sampling frequency  Hz and having   samples. In frequency domain we can define  in steps of  Hz.

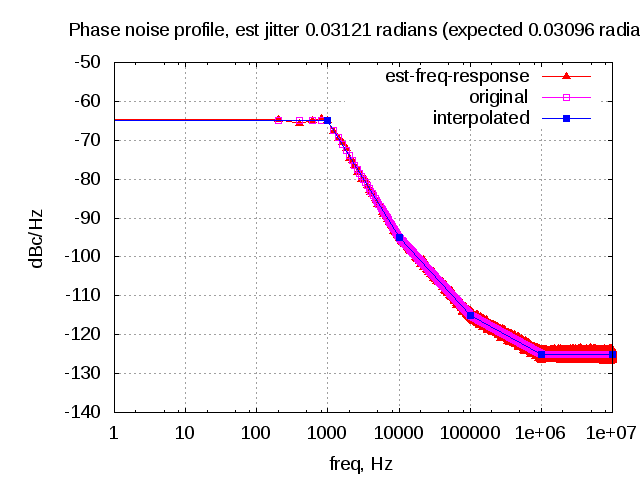
b) Consider a phase noise profile defined as follows :

freq	PSD, dBc/Hz
0	-65
1kHz	-65
10kHz	-95
100kHz	-115
1MHz	-125
10MHz	-125

 Table : Example phase noise profile

From the phase noise profile, using linear interpolation (in log10 of the frequency axis), to find the phase noise power spectral density for frequencies from  in steps of  Hz.

c) Generate a white Gaussian noise sample of length  and scale it with the phase noise power spectral density

(Scaling by  is to normalize the resolution bandwidth to unity)

d) Use ifft() to find the time domain samples.

e) On the rel samples obtained from step (d), take  to form the time domain phase noise samples.

Note :

When x is small, .

 

Example Matlab script

% Script for simulating the an example phase noise profile 
% ----------------------------------------------------------

clear all; close all;
fs_Hz    = 20e6;
N        = 10^5;
nIter    = 100;

% phase noise profile
psd_f_hz           = [  0  1e3  1e4  1e5  1e6  10e6];
psd_val_dbc_per_hz = [-65  -65  -95 -115 -125  -125];

% defining the frequency vector
freq_v_Hz = [0:N/2]/N*fs_Hz;
delta_f   = fs_Hz/N;
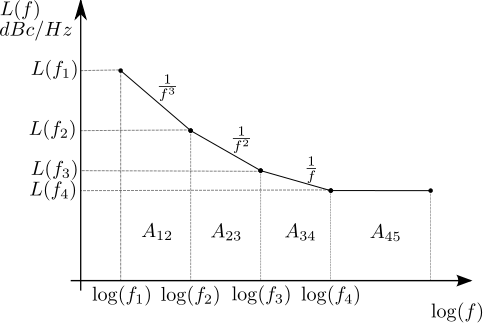
slope    = [psd_val_dbc_per_hz(2:end) - psd_val_dbc_per_hz(1:end-1) ]./...
		(log10(psd_f_hz(2:end)) - log10(psd_f_hz(1:end-1)));
constant = 10.^(psd_val_dbc_per_hz(1:end-1)/10).* ...
		(psd_f_hz(1:end-1).^(-slope/10));
integral = constant.*(psd_f_hz(2:end).^(1+slope/10) - ...
			psd_f_hz(1:end-1).^(1+slope/10) )./(1+slope/10);
%% finding the rms jitter
% finding index with slope == -10
idx = find(slope==-10);
integral(idx) = constant(idx).*(log(psd_f_hz(idx+1)) - log(psd_f_hz(idx)));
rms_jitter_radians  = sqrt(2*integral);
integrated_jitter_radians = sqrt(2*sum(integral))

% interpolating the phase noise psd values
psd_ssb_dB = -Inf*ones(1,N/2+1); % from [0:N/2]
for ii=1:length(psd_f_hz)-1
   [tt1 fl_idx ] = (min(abs(psd_f_hz(ii) - freq_v_Hz)));
   [tt2 fr_idx ] = (min(abs(psd_f_hz(ii+1) - freq_v_Hz)));	
   fvec = [freq_v_Hz(fl_idx):delta_f:freq_v_Hz(fr_idx)];
   pvec = slope(ii)*log10(fvec+eps) + psd_val_dbc_per_hz(ii) - slope(ii)*log10(psd_f_hz(ii)+eps);
   psd_ssb_dB(fl_idx:fr_idx) = pvec;
end

% forming the full vector from [-N/2:-1 0:N/2-1 ]/N*fs_Hz
psd_dB                  = -Inf*ones(1,N);
psd_dB([-N/2:-1]+N/2+1) = psd_ssb_dB([N/2+1:-1:2]);
psd_dB([0:N/2-1]+N/2+1) = psd_ssb_dB(1:N/2);

psd_linear = 10.^(psd_dB/20);

for (jj = 1:nIter)
   % defining frequency vector
   phase_noise_freq       = 1/sqrt(2)*(randn(1,N) + j*randn(1,N));
   phase_noise_freq_scale = N*sqrt(delta_f)*phase_noise_freq;
   phase_noise_freq_psd   = phase_noise_freq_scale .*psd_linear;

   % converting to time domain
   phase_noise_td      = ifft(fftshift(phase_noise_freq_psd));
   pn_td               = exp(j*(sqrt(2)*real(phase_noise_td)));

   % for estimating jitter and plotting 
   pn_without_carrier  = (pn_td - 1);
   est_jitter_pwr_radians(jj) = mean(pn_without_carrier.*conj(pn_without_carrier));

   hF           = 1/(N*sqrt(delta_f))*fft(pn_without_carrier,N);
   hFPwr(jj,:)  = hF.*conj(hF);
end

est_integrated_jitter_radians = sqrt(mean(est_jitter_pwr_radians));
title_str = sprintf('Phase noise profile, est jitter %2.5f radians (expected %2.5f radians)', est_integrated_jitter_radians, integrated_jitter_radians);

figure
semilogx( [-N/2:N/2-1]/N*fs_Hz, 10*log10(fftshift(mean(hFPwr))), 'r^-' );
hold on;grid on;
semilogx([0:N/2]/N*fs_Hz,psd_ssb_dB,'mp-');
semilogx(psd_f_hz,psd_val_dbc_per_hz,'bs-');
legend('est-freq-response','original','interpolated');
xlabel('freq, Hz'); ylabel('dBc/Hz');
axis([1 10e6 -140 -50]); title(title_str);

 Figure : Example phase noise profile (expected and simulated)

Summary

The above approach seems to allow a way to model an arbitrary phase noise power spectral density. However, the fact that this approach needs a large ifft() of length can potentially slow down the simulation.

 

References

[1] Phase Noise by Alex Bar-Guy, 27 Oct 2005 (Updated 08 Dec 2005) http://www.mathworks.com/matlabcentral/fileexchange/8844-phase-noise

[2]  Baseband-equivalent phase noise model, Submitted by Markus Nentwig on Dec 18 2011

http://www.dsprelated.com/showcode/246.php

Tagged as: noise, phase_noise

D id you like this article? Make sure that you do not miss a new article by subscribing to RSS feed OR subscribing to e-mail newsletter. Note: Subscribing via e-mail entitles you to download the free e-Book on BER of BPSK/QPSK/16QAM/16PSK in AWGN.