BER for BPSK in ISI channel with Zero Forcing equalization

In the past, we had discussed BER for BPSK in flat fading Rayleigh channel. In this post, lets discuss a frequency selective channel with the use of Zero Forcing (ZF) equalization to compensate for the inter symbol interference (ISI). For simplifying the discussion, we will assume that there is no pulse shaping at the transmitter. The ISI channel is assumed to be a fixed 3 tap channel.

Transmit symbol

Let the transmit symbols be modeled as

, where

is the symbol period,

is the symbol to transmit,

is the transmit filter,

is the symbol index and

is the output waveform.

For simplicity, lets assume that the transmit pulse shaping filter is not present, i.e .

So the transmit symbols can be modeled by the discrete time equivalent

Figure: Transmit symbols

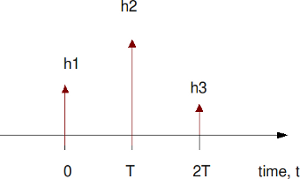
Channel Model

Lets us assume the channel to be a 3 tap multipath channel with spacing i.e.

Figure: Channel model (3 tap multipath)

In addition to the multipath channel, the received signal gets corrupted by noise , typically referred to as Additive White Gaussian Noise (AWGN). The values of the noise follows the Gaussian probability distribution function, with

mean and

variance .

The received signal is

, where

is the convolution operator.

Zero Forcing Equalization

Objective of Zero Forcing Equalization is to find a set of filter coefficients which can make .

After equalization

.

Note:

The term causes noise amplification resulting poorer bit error rate performance.

Deriving the equalization coefficients

From the post on toeplitz matrix,we know that convolution operation can be represented as matrix multiplication.

% Matlab code for using Toeplitz matrix for convolution
clear all
x = [1:3];
h = [4:6];
xM = toeplitz([x zeros(1,length(h)-1) ], [x(1) zeros(1,length(h)-1) ]);
y1 = xM*h';
y2 = conv(x,h);
diff = y1'-y2
diff = [  0   0   0   0   0 ]

Using similar matrix algebra and assuming that the coefficients has 3 taps, the equation can be equivalently represented as,

Solving for , we have

.

If we assume that has 5 taps,

Solving for , we have

.

Example

% Assuming a 3 tap channel as follows
ht = [0.2 0.9 0.3];
L = length(ht);
kk = 1;
hM = toeplitz([ht([2:end]) zeros(1,2*kk+1-L+1)], [ ht([2:-1:1]) zeros(1,2*kk+1-L+1) ]);
d  = zeros(1,2*kk+1);
d(kk+1) = 1;
c  = [inv(hM)*d.'].';

The frequency response of the channel and the equalizer are shown below:

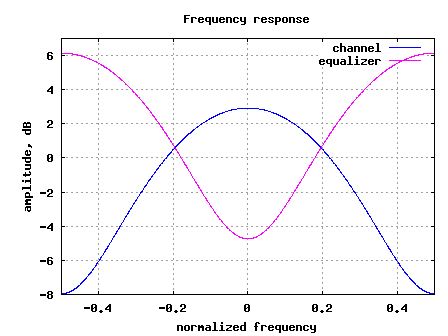
Figure: Frequency response of the channel and the equalizer

Simulation Model

Click here to download: Matlab/Octave script for computing BER for BPSK with 3 tap ISI channel with Zero Forcing Equalization

The attached Matlab/Octave simulation script performs the following:

(a) Generation of random binary sequence

(b) BPSK modulation i.e bit 0 represented as -1 and bit 1 represented as +1

(c) Convolving the symbols with a 3-tap fixed fading channel.

(d) Adding White Gaussian Noise

(e) Computing the equalization filter at the receiver – the equalization filter is 3, 5, 7, 9 taps in length

(f) Demodulation and conversion to bits

(g) Counting the number of bit errors

(h) Repeating for multiple values of Eb/No

The simulation results are as shown in the plot below.

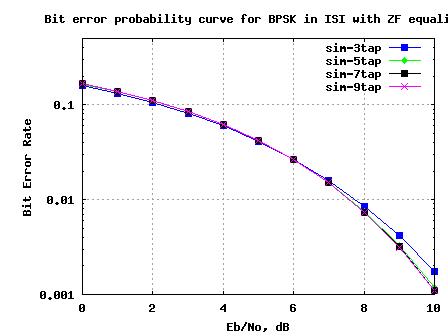
Figure: BER plot for BPSK in a 3 tap ISI channel with Zero Forcing equalizer

Observations

1. Increasing the equalizer tap length from 3 to 5 showed reasonable performance improvement.

2. Diminishing returns from improving the equalizer tap length above 5.

3. The results are poorer compared to the AWGN no multipath results. This is due to the noise amplification (see the frequency response above) by the zero forcing equalization filter.

Next step is to discuss the zero forcing equalizer in the presence of transmit pulse shaping and then move on to minimum mean square error equalizer.

Tagged as: BPSK, ISI, ZF

Related posts

1. BER for BPSK in ISI channel with MMSE equalization
2. Using Toeplitz matrices in MATLAB
3. Polyphase filters for interpolation
4. MIMO with Zero Forcing Successive Interference Cancellation equalizer
5. MIMO with Zero Forcing equalizer

D id you like this article? Make sure that you do not miss a new article by subscribing to RSS feed OR subscribing to e-mail newsletter. Note: Subscribing via e-mail entitles you to download the free e-Book on BER of BPSK/QPSK/16QAM/16PSK in AWGN.