Softbit for 16QAM

In the post on Soft Input Viterbi decoder, we had discussed BPSK modulation with convolutional coding and soft input Viterbi decoding in AWGN channel. Let us know discuss the derivation of soft bits for 16QAM modulation scheme with Gray coded bit mapping. The channel is assumed to be AWGN alone.

Gray Mapped 16-QAM constellation

In the past, we had discussed BER for 16QAM in AWGN modulation. The 4 bits in each constellation point can be considered as two bits each on independent 4-PAM modulation on I-axis and Q-axis respectively.

b0b1	I	b2b3	Q
00	-3	00	-3
01	-1	01	-1
11	+1	11	+1
10	+3	10	+3

Table: Gray coded constellation mapping for 16-QAM

16QAM modulation with Gray coded mapping

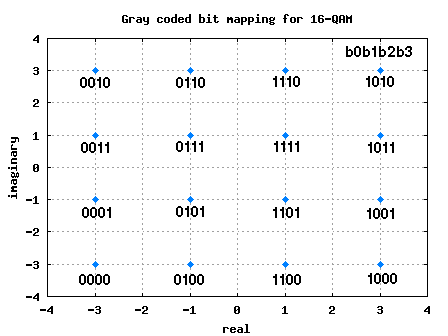
Figure: 16QAM constellation plot with Gray coded mapping

Channel Model

The received coded sequence is

$y=c + n$ , where

$c$ is the modulated coded sequence taking values in the alphabet

$\alpha_{16QAM}=\left{\pm 1+\pm 1j,\ \pm 1+\pm 3j,\\\pm 3 + \pm 3j,\ \pm 3+\pm 1j \right}$ .

$n$ is the Additive White Gaussian Noise following the probability distribution function,

$p(n) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(n-\mu)^2}{2\sigma^2}$ with mean $\mu=0$ and variance $\sigma^2 = \frac{N_0}{2}$ .

Demodulation

For demodulation, we would want to maximize the probability that the bit $b_m$ was transmitted given we received $y$ i.e $P(b_m|y)$ . This criterion is called Maximum a posteriori probability (MAP).

Using Bayes rule,

$P(b_m|y) = \frac{P(y|b_m)p(b_m)}{p(y)}$ .

Note: The probability that all constellation points occur are equally likely, so maximizing $P(b_m|y)$ is equivalent to maximizing $P(y|b_m)$ .

Soft bit for b0

The bit mapping for the bit b0 with 16QAM Gray coded mapping is shown below. We can see that when b0 toggles from 0 to 1, only the real part of the constellation is affected.

Bit maping for bit b0 is Gray coded 16QAM

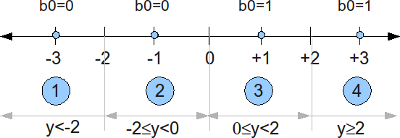
Figure: Bit b0 for 16QAM Gray coded mapping

When the b0 is 0, the real part of the QAM constellation takes values -3 or -1. The conditional probability of the received signal $y$ given b0 is 0 is,

$P(y|b_0=0) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-(y_{re}+3)^2}{2\sigma^2}} + \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-(y_{re}+1)^2}{2\sigma^2}}$ .

When the bit0 is 1, the real part of the QAM constellation takes values +1 or +3. The conditional probability given b0 is zero is,

$P(y|b_0=1) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-(y_{re}-1)^2}{2\sigma^2}} + \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-(y_{re}-3)^2}{2\sigma^2}}$ .

We can define a likelihood ratio that if

$b0=1,\ if \frac{P(y|b_0=1)}{P(y|b_0=0)}\ge0$ .

The likelihood ratio for b0 is,

$\frac{P(y|b_0=1)}{P(y|b_0=0)}=\frac{e^{\frac{-(y_{re}-1)^2}{2\sigma^2}} + e^{\frac{-(y_{re}-3)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+1)^2}{2\sigma^2}}+e^{\frac{-(y_{re}+3)^2}{2\sigma^2}}}$ .

Region #1 ( $y_{re} < -2$ )

When $y_{re} < -2$ , then we can assume that relative contribution by constellation +3 in the numerator and -1 in the denominator is less and can be ignored. So the likelihood ratio reduces to,

$\frac{P(y|b_0=1)}{P(y|b_0=0)}\approx\frac{ e^{\frac{-(y_{re}-1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+3)^2}{2\sigma^2}}}$ .

Taking logarithm on both sides,

$\begin{array}{lll}\ln\left(\frac{P(y|b_0=1)}{P(y|b_0=0)}\right)&\approx&\ln\left(\frac{ e^{\frac{-(y_{re}-1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+3)^2}{2\sigma^2}}}\right)\\&=&\frac{1}{2\sigma^2}(y_{re}+3)^2-(y_{re}-1)^2\\&=&\frac{1}{\sigma^2}4(y_{re}+1)\end{array}$ .

Region #2 ( $-2\le y_{re} <0$ ), Region #3 ( $0\le y_{re} <2$ )

When $-2\le y_{re} <0$ or $0\le y_{re} <2$ , then we can assume that relative contribution by constellation +3 in the numerator and -3 in the denominator is less and can be ignored. So the likelihood ratio reduces to,

$\frac{P(y|b_0=1)}{P(y|b_0=0)}\approx\frac{ e^{\frac{-(y_{re}-1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+1)^2}{2\sigma^2}}}$ .

Taking logarithm on both sides,

$\begin{array}{lll}\ln\left(\frac{P(y|b_0=1)}{P(y|b_0=0)}\right)&\approx&\ln\left(\frac{ e^{\frac{-(y_{re}-1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+1)^2}{2\sigma^2}}}\right)\\&=&\frac{1}{2\sigma^2}(y_{re}+1)^2-(y_{re}-1)^2\\&=&\frac{1}{\sigma^2}2r\end{array}$ .

Region #4 ( $y_{re}\ge 2$ )

If $y_{re}\ge 2$ , then we can assume that relative contribution by constellation +1 in the numerator and -3 in the denominator is less and can be ignored. So the likelihood ratio reduces to,

$\frac{P(y|b_0=1)}{P(y|b_0=0)}\approx\frac{ e^{\frac{-(y_{re}-3)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+1)^2}{2\sigma^2}}}$ .

Taking logarithm on both sides,

$\begin{array}{lll}\ln\left(\frac{P(y|b_0=1)}{P(y|b_0=0)}\right)&\approx&\ln\left(\frac{ e^{\frac{-(y_{re}-3)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+1)^2}{2\sigma^2}}}\right)\\&=&\frac{1}{2\sigma^2}(y_{re}+1)^2-(y_{re}-3)^2\\&=&\frac{1}{\sigma^2}4(y_{re}-1)\end{array}$ .

Soft bit for b1

The bit mapping for the bit b1 with 16QAM Gray coded mapping is shown below. We can see that when b0 toggles from 0 to 1, only the real part of the constellation is affected.

Gray coded 16QAM bit mapping for bit b1

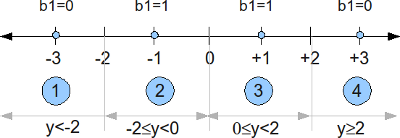
Figure: Bit b1 for 16QAM Gray coded mapping

When the b1 is zero, the real part of the QAM constellation takes values -3 or +3. The conditional probability given b0 is zero is,

$P(y|b_0=0) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-(y_{re}+3)^2}{2\sigma^2}} + \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-(y_{re}-3)^2}{2\sigma^2}}$ .

When the bit0 is 1, the real part of the QAM constellation takes values -1 or +1. The conditional probability given b0 is zero is,

$P(y|b_1=1) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-(y_{re}+1)^2}{2\sigma^2}} + \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-(y_{re}-1)^2}{2\sigma^2}}$ .

We can define a likelihood ratio that if

$b1=1,\ if \frac{P(y|b_1=1)}{P(y|b_1=0)}\ge0$ .

The likelihood ratio for b1 is,

$\frac{P(y|b_1=1)}{P(y|b_1=0)}=\frac{e^{\frac{-(y_{re}+1)^2}{2\sigma^2}} + e^{\frac{-(y_{re}-1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+3)^2}{2\sigma^2}}+e^{\frac{-(y_{re}-3)^2}{2\sigma^2}}}$ .

Region #1 ( $y_{re} < -2$ ), Region#2 ( $-2\le y_{re} <0$ )

When $y_{re} < -2$ or $-2\le y_{re} <0$ , then we can assume that relative contribution by constellation +1 in the numerator and +3 in the denominator is less and can be ignored. So the likelihood ratio reduces to,

$\frac{P(y|b_1=1)}{P(y|b_1=0)}\approx\frac{ e^{\frac{-(y_{re}+1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+3)^2}{2\sigma^2}}}$ .

Taking logarithm on both sides,

$\begin{array}{lll}\ln\left(\frac{P(y|b_1=1)}{P(y|b_1=0)}\right)&\approx&\ln\left(\frac{ e^{\frac{-(y_{re}+1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}+3)^2}{2\sigma^2}}}\right)\\&=&\frac{1}{2\sigma^2}(y_{re}+3)^2-(y_{re}+1)^2\\&=&\frac{2}{\sigma^2}(r+2)\end{array}$ .

Region #3 ( $0\le y_{re} <2$ ), Region #4 ( $y_{re}\ge 2$ )

If $0\le y_{re} <2$ or $y_{re}\ge 2$ , then we can assume that relative contribution by constellation -1 in the numerator and -3 in the denominator is less and can be ignored. So the likelihood ratio reduces to,

$\frac{P(y|b_1=1)}{P(y|b_1=0)}\approx\frac{ e^{\frac{-(y_{re}-1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}-3)^2}{2\sigma^2}}}$ .

Taking logarithm on both sides,

$\begin{array}{lll}\ln\left(\frac{P(y|b_1=1)}{P(y|b_1=0)}\right)&\approx&\ln\left(\frac{ e^{\frac{-(y_{re}-1)^2}{2\sigma^2}}}{e^{\frac{-(y_{re}-3)^2}{2\sigma^2}}}\right)\\&=&\frac{1}{2\sigma^2}(y_{re}-3)^2-(y_{re}-1)^2\\&=&\frac{2}{\sigma^2}(-y_{re}+2)\end{array}$ .

Summary

Note: As the factor $\frac{2}{\sigma^2}$ is common to all the terms, it can be removed.

The softbit for bit b0 is,

$\begin{array}{lllr}sb(b0) & = & 2(y_{re}+1), & y_{re} < -2 \\<br /> & = & y_{re}, & -2 \le y_{re} < 2\\ & = & 2(y_{re}-1), & y_{re} > 2\end{array}$ .

The softbit for bit b1 is,

$\begin{array}{lllr}sb(b1) & = & y_{re}+2, & y_{re} \le 0 \\<br /> & = & -y_{re} + 2, & y_{re} > 0\end{array}$ .

The softbit for bit b1 can be simplified to,

$\begin{array}{lllr}sb(b1) & = & -|y_{re}|+2, & \mbox{for all } y_{re}\end{array}$ .

It is easy to observe that the softbits for bits b2, b3 are identical to softbits for b0, b1 respectively except that the decisions are based on the imaginary component of the received vector $y_{im}$ .

The softbit for bit b2 is,

$\begin{array}{lllr}sb(b2) & = & 2(y_{im}+1), & y_{im} < -2 \\<br /> & = & y_{im}, & -2 \le y_{im} < 2\\ & = & 2(y_{im}-1), & y_{im} > 2\end{array}$ .

The softbit for bit b3 is,

$\begin{array}{lllr}sb(b3) & = & -|y_{im}|+2, & \mbox{for all }y_{im}\end{array}$ .

As described in the paper, Simplified Soft-Output Demapper for Binary Interleaved COFDM with Application to HIPERLAN/2, Filippo Tosato1, Paola Bisaglia, HPL-2001-246 October 10th , 2001, the term

$2(y_{re}+1) \approx = y_{re}$ and

$2(y_{im}+1) \approx = y_{im}$ ,

This simplification avoids the need for having a threshold check in the receiver for sofbits b0 and b2 respectively.

Reference

Simplified Soft-Output Demapper for Binary Interleaved COFDM with Application to HIPERLAN/2, Filippo Tosato1, Paola Bisaglia, HPL-2001-246 October 10th , 2001

Tagged as: 16-QAM, QAM, Viterbi

D id you like this article? Make sure that you do not miss a new article by subscribing to RSS feed OR subscribing to e-mail newsletter. Note: Subscribing via e-mail entitles you to download the free e-Book on BER of BPSK/QPSK/16QAM/16PSK in AWGN.

{ 14 comments… read them below or add one }

1 robin July 6, 2009 at 6:00 pm

clearly.
thx a lot.

2 invizible July 20, 2009 at 2:19 pm

Hi Krishna!
I hope you are doing great. I have a very basic question. I am implementing OFDM system in matlab. r_k are my received symbols and s_k are my transmitted symbols, where k is the subcarrier index. Now at the receiver, after zero forcing equalizer, I want to find the variance i.e. var = E[|r_k - s_k|²], but I dont know how to implement this equation in matlab… kindly help
best regards,
invizi.

3 Krishna Pillai July 20, 2009 at 7:24 pm

@invizible: Thanks, am doing good. Hope you are fine too.

Well, in Matlab mean(abs(r_k – s_k).^2) should do the job for you.

4 invizible July 21, 2009 at 1:00 pm: Thanks alot … you are doing a very fine job … Krishna the great

5 Zhongren Cao July 20, 2009 at 10:01 pm

Hey Krishna,

Along the line of soft decoding, do you plan to write some articles on chase combining?

Thanks,
Zhongren

6 Krishna Pillai July 24, 2009 at 3:54 am: @Zhongren: I have not yet tried modeling any automatic repeat request (ARQ) schemes and correspondingly chase combining. I will add to my to-do list.

7 ruoyu September 8, 2009 at 2:00 pm

thanks,it’s a clear,simple computing of LLR.

8 Krishna Sankar September 9, 2009 at 5:54 am: @ruoyu: Glad

9 sam March 28, 2010 at 9:05 pm

hello krishna
i have a question , why two and four phase psk have same figure in plotting of SNR (per bit)(horizontal axis) in term Pb (probability of error)(vertical axis)? in page 225 of digital communication proakis 5ed
any good reference for complete explanation

10 Krishna Sankar March 29, 2010 at 6:34 am: @sam: Well with 4-PSK, the modulation is performed on two orthogonal dimensions. Hence the noise added on one dimension will not affect the other. Hence the BER is the same.

11 xiaonaren April 8, 2010 at 2:18 pm

hello krishna
I have a question, as for the softbit for 16-QAM, if the channel is not AWGN but exponentical decay , how can I get the softbit?
Thanks,
xiaonaren

12 Krishna Sankar April 14, 2010 at 5:18 am: @xiaonaren: Am not sure of the case where there is ISI. However, if its only flat fading, the above equations with additional scaling factor for channel gain should hold good

13 Mohamed Hedi June 20, 2010 at 12:48 pm

Hi,
I am working on a QAM-16 modem,
can you help me please to implement it on MTLAB
regards

14 Krishna Sankar June 21, 2010 at 5:45 am: @Mohamed Hedi: You can look at articles @ http://www.dsplog.com/tag/qam
Hopefully, it helps.

Softbit for 16QAM

Gray Mapped 16-QAM constellation

Channel Model

Demodulation

Soft bit for b0

Region #1 ( $y_{re} < -2$ )

Region #2 ( $-2\le y_{re} <0$ ), Region #3 ( $0\le y_{re} <2$ )

Region #4 ( $y_{re}\ge 2$ )

Soft bit for b1

Region #1 ( $y_{re} < -2$ ), Region#2 ( $-2\le y_{re} <0$ )

Region #3 ( $0\le y_{re} <2$ ), Region #4 ( $y_{re}\ge 2$ )

Summary

Reference

Related posts

Subscribe

Categories

Archives

Top Rated posts

Recent Posts

Comments

DSP

FPGA

General

Softbit for 16QAM

Gray Mapped 16-QAM constellation

Channel Model

Demodulation

Soft bit for b0

Region #1 ()

Region #2 (), Region #3 ()

Region #4 ()

Soft bit for b1

Region #1 (), Region#2 ()

Region #3 (), Region #4 ()

Summary

Reference

Related posts

Subscribe

Tag

Categories

Archives

Top Rated posts

Recent Posts

Comments

DSP

FPGA

General

Region #1 ( $y_{re} < -2$ )

Region #2 ( $-2\le y_{re} <0$ ), Region #3 ( $0\le y_{re} <2$ )

Region #4 ( $y_{re}\ge 2$ )

Region #1 ( $y_{re} < -2$ ), Region#2 ( $-2\le y_{re} <0$ )

Region #3 ( $0\le y_{re} <2$ ), Region #4 ( $y_{re}\ge 2$ )