MIMO with Zero Forcing equalizer

Krishna Sankar16 years ago12 years ago15412 mins

We had discussed three Single Input Multiple Output (SIMO also known as receive diversity) schemes – Selection combining, Equal Gain Combining, Maximal Ratio Combining and a Multiple Input Single Output (MISO, also known as transmit diversity) scheme – Alamouti 2×1 STBC. Let us now discuss the case where there a multiple transmit antennas and multiple receive antennas resulting in the formation of a Multiple Input Multiple Output (MIMO) channel. In this post, we will restrict our discussion to a 2 transmit 2 receive antenna case (resulting in a 2×2 MIMO channel). We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.

2×2 MIMO channel

In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:

1. Consider that we have a transmission sequence, for example $\{x_1, x_2, x_3, \ldots, x_n \}$

2. In normal transmission, we will be sending $x_1$ in the first time slot, $x_2$ in the second time slot, $x_3$ and so on.

3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send $x_1$ and $x_2$ from the first and second antenna. In second time slot, send $x_3$ and $x_4$ from the first and second antenna, send $x_5$ and $x_6$ in the third time slot and so on.

4. Notice that as we are grouping two symbols and sending them in one time slot, we need only $\frac{n}{2}$ time slots to complete the transmission – data rate is doubled ! 🙂

5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.

Having said this, some of you will wonder – the two transmitted symbols interfered with each other. Can we ever separate the two out? The rest of the post attempts to answer this question. 🙂

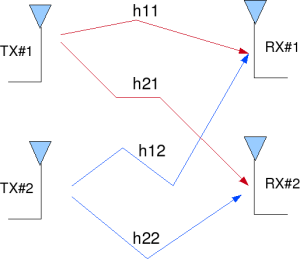
Figure: 2 Transmit 2 Receive (2×2) MIMO channel

Other Assumptions

1. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]

2. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas.

3. For the $i^{th}$ transmit antenna to $j^{th}$ receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number $h_{j,i}$ . As the channel under consideration is a Rayleigh channel, the real and imaginary parts of $h_{j,i}$ are Gaussian distributed having mean $\mu_{h_{j,i}=0$ and variance $\sigma^2_{h_{j,i}}=\frac{1}{2}$ .

4. The channel experienced between each transmit to the receive antenna is independent and randomly varying in time.

5. On the receive antenna, the noise $n$ has the Gaussian probability density function with

$p(n) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(n-\mu)^2}{2\sigma^2}$ with $\mu=0$ and $\sigma^2 = \frac{N_0}{2}$ .

7. The channel $h_{j,i}$ is known at the receiver.

Zero forcing (ZF) equalizer for 2×2 MIMO channel

Let us now try to understand the math for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is,

$y_1 =h_{1,1}x_1 + h_{1,2}x_2 + n_1 = [h_{1,1}\ h_{1,2}] \left[\begin{eqnarray}x_1 \\ x_2 \end{eqnarray}\right]+n_1$ .

The received signal on the second receive antenna is,

$y_2 = h_{2,1}x_1 + h_{2,2}x_2 + n_2 = [h_{2,1}\ h_{2,2}] \left[\begin{eqnarray}x_1 \\ x_2\end{eqnarray}\right]+n_2$ .

where

$y_1$ , $y_2$ are the received symbol on the first and second antenna respectively,

$h_{1,1}$ is the channel from $1^{st}$ transmit antenna to $1^{st}$ receive antenna,

$h_{1,2}$ is the channel from $2^{nd}$ transmit antenna to $1^{st}$ receive antenna,

$h_{2,1}$ is the channel from $1^{st}$ transmit antenna to $2^{nd}$ receive antenna,

$h_{2,2}$ is the channel from $2^{nd}$ transmit antenna to $2^{nd}$ receive antenna,

$x_1$ , $x_2$ are the transmitted symbols and

$n_1,\ n_2$ is the noise on $1^{st}, 2^{nd}$ receive antennas.

We assume that the receiver knows $h_{1,1}$ , $h_{1,2}$ , $h_{2,1}$ and $h_{2,2}$ . The receiver also knows $y_1$ and $y_2$ . The unknown s are $x_1$ and $x_2$ . Two equations and two unknowns. Can we solve it? Answer is YES. 🙂

For convenience, the above equation can be represented in matrix notation as follows:

$\begin{eqnarray}\left[\begin{eqnarray}y_1 \\ y_2\end{eqnarray}\right] & = & {\left[\begin{array}{cc}h_{1,1}& h_{1,2} \\h_{2,1}&h_{2,2}\end{array}\right]}\left[\begin{eqnarray}x_1 \\ x_2 \end{eqnarray}\right]+\left[\begin{eqnarray}n_1\\n_2 \end{eqnarray}\right]\end{eqnarray}$ .

Equivalently,

$\mathbf{y} = \mathbf{H}\mathbf{x} + \mathbf{n}$

To solve for $\mathbf{x}$ , we know that we need to find a matrix $\mathbf{W}$ which satisfies $\mathbf{WH=I}$ . The Zero Forcing (ZF) linear detector for meeting this constraint is given by,

$\mathbf{W}=\mathbf{(H^HH)^{-1}H^H}$ .

This matrix is also known as the pseudo inverse for a general m x n matrix.

The term,

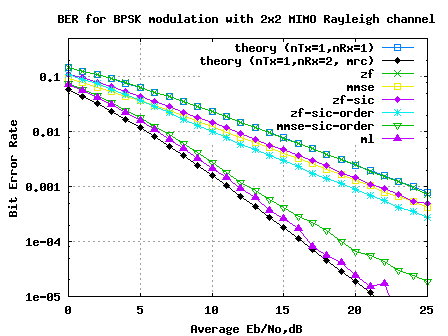
$\mathbf{H^HH} = \left[\begin{array}{cc}\ h_{1,1}^* & h_{2,1}^* \\h_{1,2}^*& h_{2,2}^*\end{array}\right]\left[\begin{array}{cc}\ h_{1,1} & h_{1,2} \\h_{2,1} & h_{2,2}\end{array}\right]=\left[\begin{array}{cc}|h_{1,1}|^2+|h_{2,1}|^2 & h_{1,1}^*h_{1,2}+h_{2,1}^*h_{2,2} \\ h_{1,2}^*h_{1,1}+h_{2,2}^*h_{2,1}& |h_{1,2}|^2+|h_{2,2}|^2\end{array}\right]$ .

BER with ZF equalizer with 2×2 MIMO

Note that the off diagonal terms in the matrix $\mathbf{H^HH}$ are not zero (Recall: The off diagonal terms where zero in Alamouti 2×1 STBC case). Because the off diagonal terms are not zero, the zero forcing equalizer tries to null out the interfering terms when performing the equalization, i.e when solving for $x_1$ the interference from $x_2$ is tried to be nulled and vice versa. While doing so, there can be amplification of noise. Hence Zero Forcing equalizer is not the best possible equalizer to do the job. However, it is simple and reasonably easy to implement.

Further, it can be seen that, following zero forcing equalization, the channel for symbol transmitted from each spatial dimension (space is antenna) is a like a 1×1 Rayleigh fading channel (Refer Section 3.3 of [WIRELESS-TSE, VISWANATH]). Hence the BER for 2×2 MIMO channel in Rayleigh fading with Zero Forcing equalization is same as the BER derived for a 1×1 channel in Rayleigh fading.

For BPSK modulation in Rayleigh fading channel, the bit error rate is derived as,

$P_{b}=\frac{1}{2}\left(1-\sqrt{\frac{(E_b/N_0)}{(E_b/N_0) +1}}\right)$ .

Simulation Model

The Matlab/Octave script performs the following

(a) Generate random binary sequence of +1’s and -1’s.

(b) Group them into pair of two symbols and send two symbols in one time slot

(d) Equalize the received symbols

(e) Perform hard decision decoding and count the bit errors

(f) Repeat for multiple values of $\frac{E_b}{N_0}$ and plot the simulation and theoretical results.

Click here to download Matlab/Octave script for simulating BER plot for 2×2 MIMO channel with ZF equalizer (BPSK modulation in Rayleigh channel)

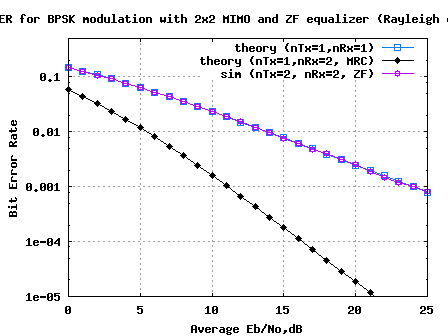
Figure: BER plot for 2×2 MIMO channel with ZF equalizer (BPSK modulation in Rayleigh channel)

Summary

1. As expected, the simulated results with a 2×2 MIMO system using BPSK modulation in Rayleigh channel is showing matching results as obtained in for a 1×1 system for BPSK modulation in Rayleigh channel.

2. As noted in Section 3.3 of [WIRELESS-TSE, VISWANATH], the Zero Forcing equalizer is not the best possible way to equalize the received symbol. The zero forcing equalizer helps us to achieve the data rate gain, but NOT take advantage of diversity gain (as we have two receive antennas).

3. We might not be able to achieve the two fold data rate improvement in all channel conditions. It can so happen that channels are correlated (the coefficients are almost the same). Hence we might not be able to solve for the two unknown transmitted symbols even if we have two received symbols.

4. It is claimed that there can be receiver structures which enables us to have both diversity gain and data rate gain. In future posts, the attempt will be to discuss receiver structures which hopefully enables us to find out approaches which will help us to keep the data rate gain, but still move from the 1×1 curve to 1×2 MRC curve. 🙂

References

[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt

[WIRELESS-TSE, VISWANATH] Fundamentals of Wireless Communication, David Tse, Pramod Viswanath

154 thoughts on “MIMO with Zero Forcing equalizer”

Raymond says:

January 28, 2013 at 4:29 am

Hi Krishna,

First of all I want to say thank you very much for writing this notes.

I have got a question about adding more antennas at the transmitting and receiving side, eg. 64*64 MIMO systems. I have tried to made modifications based on your programme but I don’t have a clue. Could you please give me some tips on possible modifications? Thank you so much!

Reply
1. Krishna Sankar says:
  
  February 1, 2013 at 5:26 am
  
  @Raymond: a 64×64 system is huge. your would want to invert the 64×64 matrix for equalization
  
  Reply
Raja says:

December 19, 2012 at 2:25 pm

Dear krishna,
Have you done any coding for MU-MIMO uplink or downlink cases. thank you

Reply
1. Krishna Sankar says:
  
  December 20, 2012 at 6:14 am
  
  @Raja: sorry, not yet
  
  Reply
Pingback: MIMO with ML equalization
Pingback: Six equalizers for V-BLAST
sandeep says:

April 30, 2012 at 2:53 pm

First of all thanks a lot for your information on matlab coding. I learnt matlab coding with the help of your codes. Thanks a lot. My question is ” I’m doing project on orthogonal space-time block codes under rayleigh channel. There is a code for this,but for a codeword of 4×4 matrix(rate=1) but i need it for8x4 matrix(rate of 0.5) and other rates of 0.75. I actually tried with QPSK modulation and demodulation, my BER vs SNR performance is of zigzag manner. Then i used your qam16 mod and demod and got 0.01 ber for an snr of 20(I hope this is not good performance)”

Reply
1. Krishna Sankar says:
  
  May 2, 2012 at 5:04 am
  
  @sandeep: well, to rule out any obvious issue, first make sure that the ber is zero when there is no noise added. once that is done, the exact performance number will depend on your coding type which is employed. try to compare with the theoretically estimated ber curves.good luck.
  
  Reply
michael says:

March 20, 2012 at 11:06 am

i have a doubt about the code:

hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term

I think that there is something wrong,because i use inv() to do the computation , the result is not the same.

I think the ‘c term’ and ‘b term ‘ should be interchanged.

Reply
1. Krishna Sankar says:
  
  March 21, 2012 at 5:03 am
  
  @michael: Is it the scaling by determinant which is missing?
  
  Reply
Binh says:

March 15, 2012 at 12:15 pm

Dear Krishna Sankar,

Does ‘ hMod = reshape(conj(h),nRx,N) ‘ do the Conjugate Transpose? I just see the conjugate work is done not the Transpose?

Reply
1. Krishna Sankar says:
  
  March 18, 2012 at 11:33 am
  
  @Binh : The ‘ does conjugate transpose.
  
  octave:3> h = [1+j 1+2j 1+3j]
  h =
  
  1 + 1i 1 + 2i 1 + 3i
  
  octave:4> h’
  ans =
  
  1 – 1i
  1 – 2i
  1 – 3i
  
  Reply
  1. michael says:
    
    March 20, 2012 at 11:41 am
    
    I also cannot find that it does the transpose operation.
    In my code ,it really just do the conj operation !
    
    thanks in advance
    
    Reply
    1. Krishna Sankar says:
      
      March 21, 2012 at 5:03 am
      
      @michael: Hmm.. not sure how to debug. hope you found the answer
      
      Reply
Neethu Alex says:

March 2, 2012 at 3:35 pm

Sir,
could u please tel me why 4×4 is not better than 2×2……

Reply
1. Krishna Sankar says:
  
  March 5, 2012 at 5:39 am
  
  @Neethu: Well, getting a sufficiently uncorrelated channel to support 4 spatial streams is more difficult than to support 2 spatial streams
  
  Reply
ash says:

December 28, 2011 at 2:46 pm

why do we use channel taps in bpsk

Reply
1. Krishna Sankar says:
  
  December 29, 2011 at 5:29 am
  
  @ash: The channel taps are not BPSK (i.e. modulation specific), rather to model the effect of reflections in wireless communication. Maybe the post on Rayleigh multipath channel model helps
  https://dsplog.com/2008/07/14/rayleigh-multipath-channel/
  
  Reply
cherifi says:

November 6, 2010 at 1:56 pm

Thanks for your great and helpful blog, I can’t have a good reuslts while Iam configure 4×4 mimo, I obtained that the 2×2 is better than 4×4
my program is:
clear
N = 10^4; % number of bits or symbols
Eb_N0_dB = [0:25]; % multiple Eb/N0 values
nTx = 2; nnTx=4;
nRx = 2; nnRx=4;
for ii = 1:length(Eb_N0_dB)

% Transmitter
ip = rand(1,N)>0.5; % generating 0,1 with equal probability
s = 2*ip-1; % BPSK modulation 0 -> -1; 1 -> 0

%2×2:
sMod = kron(s,ones(nRx,1));
sMod = reshape(sMod,[nRx,nTx,N/nTx]); % grouping in [nRx,nTx,N/NTx ] matrix
h = 1/sqrt(2)*[randn(nRx,nTx,N/nTx) + j*randn(nRx,nTx,N/nTx)]; % Rayleigh channel
n = 1/sqrt(2)*[randn(nRx,N/nTx) + j*randn(nRx,N/nTx)]; % white gaussian noise, 0dB variance
y = squeeze(sum(h.*sMod,2)) + 10^(-Eb_N0_dB(ii)/20)*n;

hCof = zeros(2,2,N/nTx);
hCof(1,1,:) = sum(h(:,2,:).*conj(h(:,2,:)),1); % d term
hCof(2,2,:) = sum(h(:,1,:).*conj(h(:,1,:)),1); % a term
hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term
hDen = ((hCof(1,1,:).*hCof(2,2,:)) – (hCof(1,2,:).*hCof(2,1,:))); % ad-bc term (det de matrix 2×2)
hDen = reshape(kron(reshape(hDen,1,N/nTx),ones(2,2)),2,2,N/nTx); % formatting for division
hInv = hCof./hDen; % inv(H^H*H)
hMod = reshape(conj(h),nRx,N); % H^H operation
yMod = kron(y,ones(1,2)); % formatting the received symbol for equalization
yMod = sum(hMod.*yMod,1); % H^H * y
yMod = kron(reshape(yMod,2,N/nTx),ones(1,2)); % formatting
yHat = sum(reshape(hInv,2,N).*yMod,1); % inv(H^H*H)*H^H*y
ipHat = real(yHat)>0;
nErr(ii) = size(find(ip- ipHat),2);

%4×4:
ssMod = kron(s,ones(nnRx,1));
ssMod = reshape(ssMod,[nnRx,nnTx,N/nnTx]);
hh= 1/sqrt(2)*[randn(nnRx,nnTx,N/nnTx) + j*randn(nnRx,nnTx,N/nnTx)]; %Rayleigh channel 4×4
nn = 1/sqrt(2)*[randn(nnRx,N/nnTx) + j*randn(nnRx,N/nnTx)]
yy = squeeze(sum(hh.*ssMod,2)) + 10^(-Eb_N0_dB(ii)/20)*nn;
hhCof = zeros(4,4,N/nnTx) ;
hhCof(1,1,:) = (sum(hh(:,2,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,2,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))+ (sum(hh(:,2,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,2,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,2,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,2,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1));
hhCof(1,2,:) = (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1));
hhCof(1,3,:) = (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1));
hhCof(1,4,:) = (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,3,:).*conj(hh(:,3,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,3,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,3,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,3,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,3,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,3,:).*conj(hh(:,3,:)),1));
hhCof(2,1,:) = (sum(hh(:,2,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))+ (sum(hh(:,2,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,2,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,2,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,2,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,2,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1));
hhCof(2,2,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1));
hhCof(2,3,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1));
hhCof(2,4,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,3,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,3,:).*conj(hh(:,1,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,3,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,3,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,3,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,3,:).*conj(hh(:,1,:)),1));
hhCof(3,1,:) = (sum(hh(:,2,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,2,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))+ (sum(hh(:,2,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))- (sum(hh(:,2,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))- (sum(hh(:,2,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,2,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1));
hhCof(3,2,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1));
hhCof(3,3,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1));
hhCof(3,4,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,3,:).*conj(hh(:,2,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,3,:).*conj(hh(:,4,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,3,:).*conj(hh(:,1,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,3,:).*conj(hh(:,4,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,4,:)),1) .* sum(hh(:,3,:).*conj(hh(:,1,:)),1))- (sum(hh(:,1,:).*conj(hh(:,4,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,3,:).*conj(hh(:,2,:)),1));
hhCof(4,1,:) = (sum(hh(:,2,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))+ (sum(hh(:,2,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))+ (sum(hh(:,2,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,2,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,2,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,2,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1));
hhCof(4,2,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,3,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,3,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,3,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1));
hhCof(4,3,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,4,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,4,:).*conj(hh(:,1,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,4,:).*conj(hh(:,2,:)),1));
hhCof(4,4,:) = (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,3,:).*conj(hh(:,3,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,3,:).*conj(hh(:,1,:)),1))+ (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,3,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,1,:)),1).* sum(hh(:,2,:).*conj(hh(:,3,:)),1) .* sum(hh(:,3,:).*conj(hh(:,2,:)),1))- (sum(hh(:,1,:).*conj(hh(:,2,:)),1).* sum(hh(:,2,:).*conj(hh(:,1,:)),1) .* sum(hh(:,3,:).*conj(hh(:,3,:)),1))- (sum(hh(:,1,:).*conj(hh(:,3,:)),1).* sum(hh(:,2,:).*conj(hh(:,2,:)),1) .* sum(hh(:,3,:).*conj(hh(:,1,:)),1));

hhDen = (hhCof(1,1,:).*hhCof(2,2,:).*hhCof(3,3,:).*hhCof(4,4,:))+(hhCof(1,1,:).*hhCof(2,3,:).*hhCof(3,4,:).*hhCof(4,2,:))+(hhCof(1,1,:).*hhCof(2,4,:).*hhCof(3,2,:).*hhCof(4,3,:))+(hhCof(1,2,:).*hhCof(2,1,:).*hhCof(3,4,:).*hhCof(4,3,:))+(hhCof(1,2,:).*hhCof(2,3,:).*hhCof(3,1,:).*hhCof(4,4,:))+(hhCof(1,2,:).*hhCof(2,4,:).*hhCof(3,3,:).*hhCof(4,1,:))+(hhCof(1,3,:).*hhCof(2,1,:).*hhCof(3,2,:).*hhCof(4,4,:))+(hhCof(1,3,:).*hhCof(2,2,:).*hhCof(3,4,:).*hhCof(4,1,:))+(hhCof(1,3,:).*hhCof(2,4,:).*hhCof(3,1,:).*hhCof(4,2,:))+(hhCof(1,4,:).*hhCof(2,1,:).*hhCof(3,3,:).*hhCof(4,2,:))+(hhCof(1,4,:).*hhCof(2,2,:).*hhCof(3,1,:).*hhCof(4,3,:))+(hhCof(1,4,:).*hhCof(2,3,:).*hhCof(3,2,:).*hhCof(4,1,:))-(hhCof(1,1,:).*hhCof(2,2,:).*hhCof(3,4,:).*hhCof(4,3,:))-(hhCof(1,1,:).*hhCof(2,3,:).*hhCof(3,2,:).*hhCof(4,4,:))-(hhCof(1,1,:).*hhCof(2,4,:).*hhCof(3,3,:).*hhCof(4,2,:))-(hhCof(1,2,:).*hhCof(2,1,:).*hhCof(3,3,:).*hhCof(4,4,:))-(hhCof(1,2,:).*hhCof(2,3,:).*hhCof(3,4,:).*hhCof(4,1,:))-(hhCof(1,2,:).*hhCof(2,4,:).*hhCof(3,1,:).*hhCof(4,3,:))-(hhCof(1,3,:).*hhCof(2,1,:).*hhCof(3,4,:).*hhCof(4,2,:))-(hhCof(1,3,:).*hhCof(2,2,:).*hhCof(3,1,:).*hhCof(4,4,:))-(hhCof(1,3,:).*hhCof(2,4,:).*hhCof(3,2,:).*hhCof(4,1,:))-(hhCof(1,4,:).*hhCof(2,1,:).*hhCof(3,2,:).*hhCof(4,3,:))-(hhCof(1,4,:).*hhCof(2,2,:).*hhCof(3,3,:).*hhCof(4,1,:))-(hhCof(1,4,:).*hhCof(2,3,:).*hhCof(3,1,:).*hhCof(4,2,:));
hhDen = reshape(kron(reshape(hhDen,1,N/nnTx),ones(4,4)),4,4,N/nnTx);
hhInv = hhCof./hhDen;
hhMod = reshape(conj(hh),nnRx,N);

yyMod = kron(yy,ones(1,4)); % formatting the received symbol for equalization
yyMod = sum(hhMod.*yyMod,1); % H^H * y
yyMod = kron(reshape(yyMod,4,N/nnTx),ones(1,4)); % formatting
yyHat = sum(reshape(hhInv,4,N).*yyMod,1); % inv(H^H*H)*H^H*y

ippHat = real(yyHat)>0;
% counting the errors

nnErr(ii) = size(find(ip- ippHat),2);
end

simBer = nErr/N; % simulated ber
simBerr = nnErr/N;
EbN0Lin = 10.^(Eb_N0_dB/10);
theoryBer_nRx1 = 0.5.*(1-1*(1+1./EbN0Lin).^(-0.5));
p = 1/2 – 1/2*(1+1./EbN0Lin).^(-1/2);
theoryBerMRC_nRx2 = p.^2.*(1+2*(1-p));

close all
figure
semilogy(Eb_N0_dB,theoryBer_nRx1,’bp-‘);
hold on
semilogy(Eb_N0_dB,theoryBerMRC_nRx2,’kd-‘);
semilogy(Eb_N0_dB,simBer,’mo-‘);
semilogy(Eb_N0_dB,simBerr,’r-*’);
axis([0 25 10^-5 0.5])
grid on
legend(‘theory (nTx=1,nRx=1)’, ‘theory (nTx=1,nRx=2, MRC)’, ‘sim (nTx=2, nRx=2, ZF)’, ‘sim (nTx=4, nRx=4, ZF)’);
xlabel(‘Average Eb/No,dB’);
ylabel(‘Bit Error Rate’);
title(‘BER for BPSK modulation with 2×2 MIMO and ZF equalizer (Rayleigh channel)’);

Reply
1. Krishna Sankar says:
  
  November 15, 2010 at 2:06 am
  
  @cherifi: Sorry, I could not look through the code. But, would not expect 4×4 to be better than 2×2.
  
  Reply
Divya says:

July 21, 2010 at 7:51 pm

Sir, am a research scholar from south India. i found your blog about 2*2 MIMO & zero forcing equalizer and is very interesting. am quite thankful to u if u suggest me some ideas to modify the code for various ocnfigurations 4*4 ,1*4 .. etc.

Reply
1. Krishna Sankar says:
  
  July 22, 2010 at 5:56 am
  
  @Divya: Thanks. Well, scaling to higher antenna configurations require you to do the channel inversion appropriately.
  
  Reply
eng_dina says:

June 17, 2010 at 3:52 am

please Mr. Krishna Sankar Iwant to build simple mimo ofdm system to simulate snr vs. ber but I want it the mimo system to be flexable not only 2×2 so ican change the number of transmitter and recievers please help me if you have the matlab code please send it to me

Reply
1. Krishna Sankar says:
  
  June 21, 2010 at 5:20 am
  
  @eng_dina: In most of the articles which I have discussed I have used 2×2 MIMO case. And to increase the speed of the Matlab simulations, I have not used inv() operation in Matlab. You can try using inv() operation and increase the speed of the simulations
  
  Reply
bouhafs says:

June 11, 2010 at 9:32 pm

H^H I d’ont now how you calculate

Reply
1. Krishna Sankar says:
  
  June 14, 2010 at 6:16 am
  
  @bouhafs: H^H is the hermitian operator i.e conjugate transpose.
  
  Reply
Matt says:

June 11, 2010 at 8:08 am

Hello

Thanks for your great and helpful blog, I am wondering if i can extend your code to the case of multiuser MIMO, for two users rather than one? just want to know weather you think it is possible so i can start working on it. big thanks again

Reply
1. Krishna Sankar says:
  
  June 14, 2010 at 6:19 am
  
  @Matt: Thanks. Yes, you can extend the code.
  
  Reply
2. kunth says:
  
  August 18, 2012 at 8:54 pm
  
  hello ,have you extended the code to multiuser ,i want to do it too.but i am new to mimo,thx!
  
  Reply
bouhafs says:

June 10, 2010 at 9:54 pm

help me please I d’ont know how you calculate the terms H^H in matlab

Reply
1. Krishna Sankar says:
  
  June 14, 2010 at 6:20 am
  
  @bouhafs: H^H is the hermitian operator i.e conjugate transpose of a matrix
  
  Reply
bouhafs says:

June 9, 2010 at 9:29 pm

please help ma how you calculate the term H^H hrrmitien in matlab

Reply
1. Krishna Sankar says:
  
  June 14, 2010 at 6:22 am
  
  @bouhafs: H^H is the Hermitian operator i.e conjugate and then transpose of a matrix
  
  Reply
bouhou says:

June 8, 2010 at 3:57 pm

hallo ,help me please i d’ont know to calculate the terms of H^H in matlab

Reply
1. Krishna Sankar says:
  
  June 14, 2010 at 6:26 am
  
  @bouhafs: H^H is the hermitian operation i.e conjugate and then transpose of a matrix
  
  Reply
bouhafs says:

June 8, 2010 at 12:37 am

help me i d’ont know how you calculate H^H IN MATLAB

Reply
1. Krishna Sankar says:
  
  June 21, 2010 at 5:59 am
  
  @bouhafs: H^H is the hermitian operation ie conjugate and then transpose.
  
  Reply
bouhafs says:

June 6, 2010 at 10:48 pm

help me please Id’ont understand how you calculate the term :H^H in MAtlab

Reply
1. Krishna Sankar says:
  
  July 2, 2012 at 5:31 am
  
  @bouhafs: hmm… you are referring to conjugate transpose i reckon – it is by doing H’
  
  Reply
mouhamed says:

June 6, 2010 at 10:46 pm

help me please i D’ont understand how you calculate the term :H^H in Matlab

Reply
1. Krishna Sankar says:
  
  July 2, 2012 at 5:30 am
  
  @mouhamed: hmm… you are referring to conjugate transpose i reckon – it is by doing H’
  
  Reply
boukhari says:

June 3, 2010 at 7:17 pm

please help me I d’ont know this ,hMod = reshape(conj(h),nRx,N);

Reply
ben says:

April 13, 2010 at 8:21 pm

Hello,

I have a question about plotting BER vs SNR in MIMO systems. Lets say i have a 2×2 MIMO system, and i perform an SVD on the channel, so i can encode and decode the signal with V and U, respectively, such that i am left with 2 uncoupled SISO channels. now each channel has its own singular value, and let us assume for now that the noise power is the same in both channels. So we have SNR1 in the first channel, and SNR2 in the second channel, and they are different.
Q1: How would you define the SNR of this system? is it the average SNR of both channels?

Now we now that according to the Water Filling algorithm, we can transmit more power (and thus, more bits) in channels with higher SNR. so if come to conclusion that the first channel can carry QPSK, and the second channel can only carry BPSK, i have different contelations in both channels… So the SNR which were calculated earlier for each channel, should now be modified in order to reflect the number of bits which are transmitted via those channels, by: SNR_bit=SNR_sym/k, where k=log_2(M).

Q2: How should plot 1 graph which describes the BER vs. SNR_bit of this system? Should i calculate SNR_bit for each SISO channel, and BER for each SISO channels separately, and the average the results?

Thanks

Reply
1. Krishna Sankar says:
  
  April 14, 2010 at 4:56 am
  
  @ben: My replies
  1.a) As I recall, when we are multiplying by V, we are not introducing any gain in the transmitter. In that case, signal power at the transmitter remains the same irrespective of multiplication by V. Agree?
  Having said that reporting SNR information from both the streams and average SNR is useful. I believe most MIMO test instruments report both
  1.b) The signal to noise ratio is independent of the constellation used. If you want to compare using Eb/N0, then yes, need to factor in the constellation
  2) Hmm…. you can defined Es/N0 = ratio of total power at tx / total noise power at rx. Then depending on the number of bits which are pumpre through, Es/N0_dB = Eb/N0_dB + 10*log10(number of bits per symbol across all tx chains)
  
  Agree? Your thoughts please.
  
  Reply
  1. ben says:
    
    April 16, 2010 at 1:53 pm
    
    1.a I agree. I want to have a single number which describes the SNR of the system. In that case, i will take the average. The only question left is which average? mean, or geometrical average?In page 12 of http://www.stanford.edu/group/cioffi/publications.html, Cioffi takes the geometric one.
    
    1.b. Since in order to compare two transmission schemes, which uses different constellations, i need to compare the BER (SER is almost meaningless, e.g., if scheme 1 uses 64QAM and scheme 2 uses BPSK….), so the x axis should read SNR_bit (=Eb/No) rather than SNR_sym (=Es/N0).
    
    2. Inside the log is the average bits per symbol over all Tx chaise? so if i Tx QPSK in stream 1, and BPSK in stream 2, than it will be qual to 1.5?
    SNR_bit=SNR_sym-10log10(1.5)?
    
    Reply
    1. Krishna Sankar says:
      
      April 18, 2010 at 2:24 pm
      
      @ben:
      1.a Well, I do not know… I need to do more reading to find out.
      1.b Well I do not think Es/N0 is meaning less… I
      2. Why 1.5? It should be 3 bits per symbol. Agree?
      
      Reply
      1. ben says:
        
        April 20, 2010 at 1:15 am
        
        2. No. QPSK is 2 bits per symbol. BPSK is 1 bit per symbol. the average is 1.5 bits.
      2. Krishna Sankar says:
        
        April 21, 2010 at 5:42 am
        
        @ben: Well, we do not need to take average. The three bits go simultaneously in air… Agree?
      3. ben says:
        
        April 25, 2010 at 9:33 pm
        
        That’s a matter of definition, whether to take the sum or the average. I would take the average but i am not saying that’s the answer.
      4. Krishna Sankar says:
        
        April 26, 2010 at 6:20 am
        
        @ben: Hmm… true.
ysn says:

April 11, 2010 at 11:47 am

Wow. Your blog is very useful for me. I’ll come here and try to catch up what you did before. Great!!

Reply
1. Krishna Sankar says:
  
  April 14, 2010 at 5:02 am
  
  @ysn: Glad
  
  Reply
Jamil says:

April 8, 2010 at 10:32 pm

Hi there,
good day. Can you please check these two lines of your code again?

hCof(2,1,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % c term
hCof(1,2,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % b term

I have done the calculation and my calculation says it should be

hCof(2,1,:) = -sum(h(:,1,:).*conj(h(:,2,:)),1); % c term
hCof(1,2,:) = -sum(h(:,2,:).*conj(h(:,1,:)),1); % b term

Thanks in advance.

Reply
1. Krishna Sankar says:
  
  April 14, 2010 at 5:25 am
  
  @Jamil: Hmm… why do you say its wrong. Recall, its co-factor
  
  Reply
Joseba says:

March 18, 2010 at 3:32 pm

hey Krishna, congratulations for the blog.

Could you recommend me some info about correlation between fast and slow fading ??
Rayleigh for fast fading.
Log-normal for shadowing.
Thank you!

Reply
1. Krishna Sankar says:
  
  March 28, 2010 at 2:21 pm
  
  @Joseba: With fast fading, the channel varies quickly over time.
  With slow fading, the channel varies slowly over time
  
  Reply
pravindra kumar says:

February 24, 2010 at 3:59 pm

can you help me getting mat lab code for rake receiver

Reply
1. Krishna Sankar says:
  
  March 31, 2010 at 5:12 am
  
  @ pravindra kumar: I have not made any posts on rake receiver.
  
  Reply
Pushpa says:

February 1, 2010 at 9:07 pm

Interesting article.
Can you help me in getting MATLAB code for MIMO frame synchronization?

Reply
1. Krishna Sankar says:
  
  April 4, 2010 at 4:31 am
  
  @Pushpa: You may ask queries
  
  Reply
Sadaf says:

January 7, 2010 at 4:48 pm

hey karishna your codes and articls help alooooooooot
thank you sooo very much 🙂

Reply
AceKris says:

January 6, 2010 at 8:11 pm

How can I make sure that E[||H|| * ||H||] =1 ?
ie Expectation of square of Mod of the Channel matrix is equal to one.
This is the first condition that has to be met before I start to simulate.
Is the term [||H|| * ||H||] relating to the a single channel realization or an ensemble of them. In anycase how do I generate H satisfying the above condition and verify this the same. H is a Rayleigh fading channel initially and later on (not related to the first one) I will have to look into the cascaded rayleigh fading channel.

Thanks and Regards

Reply
joey says:

January 5, 2010 at 8:21 pm

have u considered the 4×4 case. how could thisbe extended to it

Reply
bouhafs says:

December 13, 2009 at 7:33 pm

help me please :my question is I need the matlab program calculates the’binary ‘error rate ”BER”of systems (SISO, Simo, miso mimo) COMPARISON

Reply
bouhafs says:

December 13, 2009 at 7:31 pm

I need the matlab program calculates the”error rate”of binary systems (SISO, Simo, miso mimo) COMPARISON

Reply
1. Krishna Sankar says:
  
  December 22, 2009 at 5:33 am
  
  @bouhafs: Please have a look at
  https://dsplog.com/tag/diversity/
  https://dsplog.com/tag/mimo
  
  Reply
  1. Vineet Singh says:
    
    March 12, 2010 at 8:29 am
    
    Hi Krishna thanks for this post,
    
    I had a few doubt about channel EVM as I am working on 802.11n
    
    lets say I have 2 streams of Data which are coupled using a Q matrix and are transmitted. Then,
    Y=H[]*Q[]*S[]
    by solving for S[] I am able to calculate the stream EVM
    -but how do I calculate channel EVM ?
    -is the Q[] matrix known at the receiver
    -is it possible to extract Q[] matrix at the receiver
    
    Reply
    1. Krishna Sankar says:
      
      March 28, 2010 at 3:54 pm
      
      @Vineet Singh: My replies:
      a) Whats your definition of channel EVM? Average EVN across streams?
      b) Typically no. Q matrix forms part of the channel estimate at the receiver.
      c) see above
      
      Reply
greg says:

November 24, 2009 at 11:10 pm

have you thought of CDMA instead of QAM for your MIMO work

Reply
1. Krishna Sankar says:
  
  December 7, 2009 at 4:23 am
  
  @greg: Well, I do not understand how CDMA can be substituted for QAM. CDMA is a multiuser technique where users are separated by codes, whereas QAM is a amplitude+phase modulation technique.
  
  Reply
greg says:

November 24, 2009 at 8:27 pm

have you tried adapting this bpsk signal to a multi-user cdma signal

Reply
1. Krishna Sankar says:
  
  December 7, 2009 at 4:21 am
  
  @greg: Sorry, no.
  
  Reply
peet says:

November 21, 2009 at 7:38 pm

Hi everybody;

my question is: If we use the same technique (e.g spatial multiplexing with the ZF receiver, or Alamouti scheme ) in the conventional MIMO performing over the flat fading channel and in MIMO-OFDM performing over the frequency selective channel, should be the results same?

I mean,… MIMO is designed for flat fading channels and OFDM transform frequency selective channel into several flat fading channel so the performance should be same, but I am not sure…

Can you please share comments on that aspect?

Reply
1. Krishna Sankar says:
  
  December 6, 2009 at 4:29 pm
  
  @peet: Yes. The usage of OFDM need not change the underlying BER.
  Please check the post on
  a) BER for BPSK in AWGN (with OFDM)
  https://dsplog.com/2008/06/10/ofdm-bpsk-bit-error/
  b) BER for BPSK in multipath channel with OFDM (same as flat fading Rayleigh channel)
  https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
  
  Reply
  1. peet says:
    
    January 26, 2010 at 2:12 pm
    
    thanks!!!….
    
    Reply
boukhari says:

November 15, 2009 at 3:34 pm

why you used the signe negatif (-) in 10^(-Eb_N0_dB(ii)/20)

Reply
1. Krishna Sankar says:
  
  December 3, 2009 at 5:41 am
  
  @boukhari: To make the noise power to be lower than the signal power
  
  Reply
bopuhafs says:

November 12, 2009 at 9:23 pm

pourqoui vous etuliser le signe moin (-) dans 10^(-Eb_N0_dB(ii)/20)

Reply
1. Krishna Sankar says:
  
  December 3, 2009 at 5:19 am
  
  @bopuhafs: To make the noise power to be lower than the signal power
  
  Reply
jhon says:

November 1, 2009 at 5:32 pm

Hi krishna
Nice blog sir…i have only one doubt..

you are using
Inverse of a [2×2] matrix [a b; c d] = 1/(ad-bc)[d -b;-c a]

method to calculate inverse of (H^H*H)..

My question is since we are finding invers of 2X2 Matrix.. why cant we use

Inverse of a [2×2] matrix [a b; c d] = 1/(ad-bc)[d -b;-c a]

method directly to calculate inverse..

why are we going through

(H^H*H)^-1 *H^H route to calculate inverse..

i am sure there is some reason for that

Thanks

Reply
1. Krishna Sankar says:
  
  November 8, 2009 at 8:36 am
  
  @jhon: 1/H is same as H^H/(H^H*H) i.e multiplying by H^H in numerator and denominator. This makes the matrix general for any non square matrix.
  Just a quick matlab code snippet:
  h = rand(2,2)+j*rand(2,2)
  w1 = inv(h’*h)*h’
  w2 = inv(h)
  
  can see w1 and w2 are same.
  
  Reply
minh says:

October 24, 2009 at 5:17 pm

hi Krishna Sankar, you do all the simulations in flat-fading environment, how about frequency selective channels which are more realistic than the former? In fact, I use ITU channel models in my simulation but it’s difficult to me to apply your codes with more taps. Would you please help me with that problem. Thank you in advance

Reply
1. aydar says:
  
  October 26, 2009 at 7:19 pm
  
  Well, i think there is no formula for uncoded BER at multi-tap Rayleigh fading channels 😉
  what will change is that if you perform equalization in time domain then you would have to do filtering (convolution) which is of course more complex than simple multiplication for one-tap fading, but if you use systems like LTE, WiMAX (OFDM, SC-FDMA based) where you have cyclic prefix and freq.domain pilots for channel estimation then there is no problem for simple frequency domain equalization.
  Another thing, ITU channel were originally for SISO systems, they have no information about spatial correlation between antennas (antenna spacing, polarization, angular spread, AoA etc.). But this model can be extended to MIMO channel models with the definition of a per-tap spatial correlation.
  
  Reply
  1. Krishna Sankar says:
    
    November 8, 2009 at 7:14 am
    
    @aydar: Ok
    
    Reply
2. Krishna Sankar says:
  
  October 27, 2009 at 5:38 am
  
  @minh: Adding simulations with frequency selective channel is my next step
  
  Reply
chen says:

October 16, 2009 at 7:29 pm

Tow questions about your code:
Q1, I think the channel need to be normalized which means h*conj(h’)=1, but it seems you did not do that, how do you think about the channel matrix normalization as I described.

Q2, To calculate the inverse matrix, in your code, why do not you directly use the matlab ‘inv()’ method but implement your self with a block of code?

Reply
1. Krishna Sankar says:
  
  October 17, 2009 at 4:18 am
  
  @chen: My replies:
  1/ The E{h*h’} over all channel realization (and not per realization) is unity.
  
  2/ As I recall, the inv() operator works only a for two dimensional matrix, and I would have to put a for loop to perform the equalization for all symbols. To speeden things up, I used my own inv() and performed the whole story using matrix algebra.
  
  Reply
Street hawk says:

August 31, 2009 at 6:32 pm

If I consider the SIMO case (1 Tx * 2 Rx), then what would be the Zero Forcing equalization matrix W?

And also for SIMO case with correlated fading which receiver structure would be better, i.e. Zero forcing/ MMSE or other kind?

Reply
1. Krishna Sankar says:
  
  September 7, 2009 at 5:31 am
  
  @Street hawk: If you have 1 transmit and 2 receive antennas and the channel is flat fading, then the ZF equalization structure reduces to Maximal Ratio Combining receiver.
  https://dsplog.com/2008/09/28/maximal-ratio-combining/
  
  Note: If you have only one transmit antenna, then there is no interference to suppress.
  
  Reply
  1. aydar says:
    
    October 26, 2009 at 6:50 pm
    
    Hi, Krishna.
    
    That what was bothering me for some long time – difference between ZF and MRC. So, you mean there is no MRC for MIMO?
    
    @Street hawk: well, if you have correlated fading then probably ML-based receivers would be a good choice. Or you could use correlation in order to perform beamforming to suppress inter-cell interference (like IRC receiver based on e.g. MMSE or MLD).
    
    Cheers
    
    Reply
    1. Krishna Sankar says:
      
      November 8, 2009 at 7:13 am
      
      @aydar: If there are multiple copies of the same information coming even in a MIMO link, we need to use MRC. For eg, a three receive, 2 transmit case.
      
      Reply
sam2 says:

August 25, 2009 at 11:24 pm

I agree with you
your answer seems to be right
thank u Mr krishna

Reply
mohanad says:

August 24, 2009 at 10:59 pm

It is honor to me to know such a vast experience man like you ….
Thanks for all special efforts you have done ….

Reply
sam2 says:

August 23, 2009 at 8:03 pm

Hi Mr krishna
I have an question about pseudo inverse matrix;
We know that we want to get an identity matrix from the equation WH=I.
So we can get the same result by using another equation which is
W=inv(H) , because [ inv(H)*H=I ]
(I consider this equation[W= inv(H)*H ] in my work and it gave me the same result.)
Can u pls explain why we can not use such equation??

Reply
1. Krishna Sankar says:
  
  August 24, 2009 at 5:04 am
  
  @sam2: The inv(H) is not defined for a non-square matrix. Hence the pseudo inverse is a more general definition which works for non-square matrix, and scales down to inverse operation for a square matrix.
  Agree?
  
  Reply
  1. aydar says:
    
    October 26, 2009 at 6:26 pm
    
    Yep. You can use inv(H) only when the number of Tx and Rx antennas are equal.
    
    Reply
    1. Krishna Sankar says:
      
      November 7, 2009 at 7:13 am
      
      @aydar: agree. we use pseudo inverse for non-square channels
      
      Reply
mohanad says:

August 19, 2009 at 7:53 pm

Hi krishna…
Can you please tell me Why you are using
y = squeeze(sum(h.*sMod,2)) + 10^(-Eb_N0_dB(ii)/20)*n;
instead of :-
y = squeeze(sum(h.*sMod,1)) + 10^(-Eb_N0_dB(ii)/20)*n;
becauase the using of sum(s,2) will sum the raws of information bits
like this:-
ip =[0 0 1 1];
s=[-1 -1 1 1];
x=sum(s,2)
will result in x=0 and that will not make any sense to me?

Reply
1. Krishna Sankar says:
  
  August 22, 2009 at 5:09 am
  
  @mohanad: The way the matrix multiplication is organized for each time slot is as follows:
  h = [h11 h12 ; h21; h22] and s = [s1 s2;s1 s2]
  We know that y = [h11*s1 + h12s2; h21*s1 + h22*s2]
  So, how do we achieve that?
  We do a dot product of h and s, and the sum in the column dimension. To the sum in the column dimension, we have the parameter sum(,2).
  
  Hope this helps.
  
  Reply
SARA' says:

August 10, 2009 at 2:03 pm

Hi Krishna,

Thanks very much for the reply. The case that am considering is that
y1=x1+x2+n1
y2=x1+x2+n2
the channel is AWGN channel and I want to apply the ZF or MMSE equilizer to de-multiplex the channels. I this case, I assume that h11, h12, h21 and h22 are equal to 1. Therefore, the inverse of the channel matrix will be INF?
If you could help me to understand how to apply the MIMO detectors for AWGN channel?

for the two parallel AWGN channel
y1=x1+n1
y2+x2+n2

Thanks very much for the reply
waiting for your kind answer

Reply
1. Krishna Sankar says:
  
  August 11, 2009 at 5:09 am
  
  @SARA: If you have
  y1=x1+x2+n1
  y2=x1+x2+n2
  the you wont be able to solve for x1 and x2, given that you know y1 and y2. Think of your linear algebra classes. To solve for two unknowns (x1, x2), we need two equations (y1, y2). If the two equations carry ‘same/similar’ information, then there is no way that we can use them for resolving y1, y2. In MIMO communication parlance, having such a channel is called rank deficient channel.
  
  Reply
2. aydar says:
  
  October 26, 2009 at 6:19 pm
  
  The problem you have is that you assume your both MIMO users (if it spatial MIMO case for example) have identical channel. That means both MIMO users are completely correlated. Your channel matrix is [1 1 ; 1 1] => you cant perform pseudoinverse inv(H^H*H). what you could do is set a phase difference between Rx antennas for one user, let’s say its ‘pi’, so your channel would be H=[1 1; 1 -1] => fully uncorrelated. It is a common problem for MMSE/ZF receivers when channels are correlated. Whereas, MLD could still exploit symbol constellation and outperform MMSE/ZF.
  
  Reply
  1. Krishna Sankar says:
    
    November 7, 2009 at 7:12 am
    
    @aydar: In general, I agree with the intent of the comment. However, just to add that I have not assumed that the channel matrix is identical. I assume that the channel matrix takes tap from Rayleigh distributed channel.
    
    Reply
  2. aydar says:
    
    November 12, 2009 at 5:51 pm
    
    oopps sorry, i think H=[1 1; 1 -1] IS still correlated, but anyway we can perform inverse (you can think of it as MMSE performs spatial separation or beamforming).
    
    Reply
SARA' says:

August 5, 2009 at 5:57 pm

Hi Krishna,
Thanks very much for the intersting topics. Could I ask what will be the case if we have AWGN channel. In this case h11, h12, h21 and h22 will be 1. and the inverse of H will Inf.
Could you explain in more details how this could be solved for AWGN channel
Regards

Reply
1. Krishna Sankar says:
  
  August 10, 2009 at 5:49 am
  
  @SARA: If we assume that the AWGN channel is formed by connecting via cable, then we can assume that h11=1, h22=1, h12=0, h21=0.
  i.e. formation of two parallel AWGN channels. Agree?
  
  Reply
hamidreza says:

August 2, 2009 at 2:14 am

hello
my name is hamidreza
i am communication student
i work on mimo channel and i need mimo-ofdm matlab code
i would appreciate your help

Reply
1. Krishna Sankar says:
  
  August 5, 2009 at 5:50 am
  
  @hamidreza: Glad to hear from you. Though I have not discussed posts on MIMO + OFDM, I have posts discussing OFDM and MIMO independently @
  https://dsplog.com/tag/ofdm
  https://dsplog.com/tag/mimo
  
  Hope this helps
  
  Reply
amrali says:

August 2, 2009 at 2:06 am

Hi, you always consider
n = 1/sqrt(2)*[randn(nRx,N/nTx) + j*randn(nRx,N/nTx)]; % white gaussian noise, 0dB variance

AWGN=10^(-Eb_N0_dB(ii)/20)*n;

WHY ?
why not , AWGN=sqrt(10^(-Eb_N0_dB(ii)/10))*n?
Thanx

Reply
1. Krishna Sankar says:
  
  August 5, 2009 at 5:49 am
  
  @amrali: The noise signal n is a voltage signal. So when we convert the dB ratio to be applied to a voltage signal, the conversion happens by 10^(dB/20). Hope this helps.
  
  Reply
khattak says:

July 21, 2009 at 5:48 pm

ok thanks

Reply
Khattak says:

July 20, 2009 at 4:13 pm

Thanks Krishna i got a lot of help from your blog and i am realy very immpressed of you. Can you tell me how to modfiy your code in case I want to use it for 4×4 and 4×3 MIMO system.

Reply
1. Krishna Pillai says:
  
  July 20, 2009 at 7:28 pm
  
  @Khattak: Thanks. Well, I have not written posts on the 4×3 or 4×4 MIMO systems. Anyhow, I hope that you will be able to adapt the existing code to the above configurations. Good luck for you algorithm explorations.
  
  Reply
Saria says:

July 6, 2009 at 8:26 pm

Dear Mr. Krishna, you are really helping students a lot. Please, I would like to know, why you used the operation sum(h(:,2,:).*conj(h(:,2,:)),1);to calculate each of the cofficents, because c*conj(c) will result in (abs(C)).^2 or in other worlds the magintude squared of each of the column elements. also, why taking summation?. Thank you again and best wishes.

Reply
1. Krishna Pillai says:
  
  July 15, 2009 at 4:36 am
  
  @Saria: If you see the equation, the term (H^H*H) has |h_{1,2}|^2 + |h_{2,2}|^2. Hence the need for the sum.
  
  Reply
Rahul says:

June 16, 2009 at 5:28 pm

Hi,
Can you tell me how to modfiy your code in cas I want to use it for a general Nt x Nr case and with 16 QAM Modulation..
Both for ZF and MMSE Equalizer

Reply
1. NSK says:
  
  March 12, 2010 at 10:15 am
  
  Sir Plz help in modifying the codes for sIC for 16 QAM and hence to comare the performance.
  2.Plz guide me in getting the codes for With and With out Equalizer performance.
  NSk
  
  Reply
  1. Krishna Sankar says:
    
    March 28, 2010 at 3:51 pm
    
    @NSK: Modifying for 16QAM should be reasonably easy.
    The following posts should be a good reference.
    https://dsplog.com/2008/06/05/16qam-bit-error-gray-mapping/
    https://dsplog.com/2007/12/09/symbol-error-rate-for-16-qam/
    
    Reply
amrali says:

May 26, 2009 at 3:07 am

hi , please, could give me address of books or litrature ,which talk about mimo matrix.
I want to understand the matrix operation on MIMO.

Thanx

Reply
1. Krishna Pillai says:
  
  May 31, 2009 at 8:21 pm
  
  @amrali: The book
  Fundamentals of Wireless Communication, David Tse, Pramod Viswanath has a very good discussion on MIMO matrices. Hope this helps.
  
  Reply
yazeed says:

May 18, 2009 at 12:39 am

Hi
in the case of 2×2 MIMO with ZF equalization what the changes in the case of 8×8 or 12×12 MIMO,i.e how i can find inv(H^H*H)*H.

Reply
1. Krishna Pillai says:
  
  May 20, 2009 at 5:37 am
  
  @yazeed: Well in the case of 8×8 or 12×12 MIMO, the equation still holds good. However, now you need to find the inverse of that 8×8 or 12×12 matrix.
  
  Reply
communications_engineer says:

May 15, 2009 at 9:00 pm

Hi. Can you tell me how you got this equation

W = (H^H*H)^-1 H^H

and what is means. Especially what is H^H

Its the only part that I can’t understand. How would I write if I only considered one path?

Reply
1. Krishna Pillai says:
  
  May 20, 2009 at 5:28 am
  
  @communications_engineer: The term H^H is Hermitian operator – in simple terms its the conjugate transpose of a matrix.
  If there is only one path, then the equation reduces to H*/|H|^2, where H* is the conjuagate of H. Agree?
  
  Reply
  1. communications_engineer says:
    
    May 22, 2009 at 8:36 pm
    
    Umm… I’ll try to get some references to understand more….
    
    Krishna, as I have written before I’m working on CDMA MUD, so I want to use ZF equalization (I now its not good, but only for the sake of it), so I’ll use ZF before the de-correlation (I’m using eq y1 = A1*r2 + A2*r2*sgma+noise, verdu’s book), so ZF before decision making.
    
    r = conv(ytx,chan); % received signal
    eq=ifft(fft(ytx) ./ fft(chan));
    r_eq = conv(r, eq); % equalizer output
    
    Would this be the right Matlab code to use? Where ytx is the spread signal of two users. If I use AWGN then I’ll just add wgn.
    
    I’m kinda confused as you can probably see, so any suggestions?
    
    Reply
    1. Krishna Pillai says:
      
      May 31, 2009 at 8:02 pm
      
      @communications_engineer: I did not quite understand your way of doing equalization. In equalization, we want to make the channel response close to an impulse, agree?
      
      Reply
John Titor says:

February 7, 2009 at 8:50 pm

How come the performance of ZF is the same as SISO? Since in the case of ZF, there is an interference between the transmitted symbols at each recive antenna.

Thanks alot

Reply
1. Krishna Pillai says:
  
  February 10, 2009 at 8:08 pm
  
  @John: Note that we receive two copies of the transmit symbol at the receiver (one on each receive antenna). The presence of two copies helps to achieve the ZF performance eventhough there is interference.
  Do you agree?
  
  Reply
  1. John Titor says:
    
    February 12, 2009 at 8:37 pm
    
    Yep, but since the matrix W is also applied to the noise, so there should be some noise enhancement. I think that would decrease the performance of ZF?
    
    Reply
    1. Krishna Pillai says:
      
      February 19, 2009 at 6:09 am
      
      @John: Yes, there is noise enhancement. But I would think that is case for 1×1 too. Hence 1×1 ZF can compare with 2×2 ZF.
      
      As an additional thought:
      If I see 1×1 with ZF equalization and MMSE equalization, I find that the equalized constellaion has a lower EVM/MER in the presence of MMSE. However, the raw BER is the same. I fail to understand that behaviour. Can you please share comments on that aspect?
      
      Reply
MIMO says:

February 6, 2009 at 7:49 pm

Hello Krishna,

I am researching in MIMO wideband and ISI. Could you help me and tell me some algortihm for decode.

thanks you.

Reply
Dwade says:

February 2, 2009 at 8:16 pm

Hi Krishna
Thanks a lot for the helpful comment. Really appreciate it!

Reply
1. kamran says:
  
  February 23, 2009 at 2:55 pm
  
  thanx dude
  
  Reply
Dwade says:

January 19, 2009 at 9:24 pm

Dear Krishna,
In fully correlated channel, i.e. correlation coefficient nearing 1 (0.9999) at both Tx and Rx, do you think ZF will outperform MMSE in this case?

Reply
1. Krishna Pillai says:
  
  January 22, 2009 at 3:32 am
  
  @Dwade: I do not have results to share. However, from a quick googling found the following article:
  Advanced receiver design boosts performance
  http://www.eetimes.com/news/design/showArticle.jhtml?articleID=206104566
  
  In the article, author is saying that both MMSE and ZF suffers when the channel is correlated. He is suggesting that Maximum Likelihood Decoder (MLD) performs the best in that scenario.
  
  Reply
me says:

January 14, 2009 at 9:06 pm

thanx for your articles…
hope it can help me….;-)

Reply
Sky Stradlin says:

December 15, 2008 at 12:10 am

Sorry, I mean the ZF equalizer you did in this post, is it should be ZF receiver?

Reply
1. Krishna Pillai says:
  
  December 16, 2008 at 6:05 am
  
  @Sky Stradlin: I think ZF equalizer and ZF receiver are used interchangably. 🙂
  
  Reply
Sky Stradlin says:

December 14, 2008 at 5:52 am

Zero Forcing and MMSE equalizer, is it a receiver structure? Coz i know there is ZF/MMSE receiver, so I’m confusing. Thanks

Reply
1. Krishna Pillai says:
  
  December 14, 2008 at 7:12 am
  
  @ Sky Stradlin: Yes, Zero Forcing and MMSE classifies two different types of receiver structure (with MMSE performing better than Zero Forcing in MIMO case). Can you please point me to the literature which discuss ZF/MMSE receiver.
  
  Reply
karl says:

December 13, 2008 at 2:24 pm

Krishna, why you don’t halved total transmit power for each transmit antenna like the case of alamouti matlab code and you still can compare with the 1×1 case?.

thanks.

Reply
1. Krishna Pillai says:
  
  December 13, 2008 at 6:41 pm
  
  @karl: Well, recall that in the MIMO case we require only half the time to transmit the symbols.
  
  Assuming P is the transmit power from a single antenna in a 1×1 case and we require time T to send N symbols. The energy
  consumed in E_{1×1| = PT
  For the 2×2 MIMO, the time taken is only T/2 and we assume that we transmit from both the antennas at power P each. The energy consumed is E_{2×2} = 2P*T/2 = PT
  Since the total energy consumed is the same, I think it is fair to compare with the SISO 1×1 case.
  Do you agree to my perspective? Kindly share your thoughts
  
  Reply
Krishna Pillai says:

December 2, 2008 at 6:06 am

@Jarrod: As is the case with MIMO, if there is ISI, then Zero Forcing equaliser does not be the optimal way to equalize. Conceptually ISI can be thought of as interference in the time domain where as MIMO can be thought of as interference in the spatial domain.

Reply
1. mimo says:
  
  February 6, 2009 at 5:51 pm
  
  Hello Krishna,
  
  thanks for this blog, I am researching signal processing for MIMO. I have utilized vblast, qostbc, with mmse but I don’t know that algorithm can I utilized for wideband. Could you help me? Do you have some example code for ISI?
  
  Thank you.
  
  Reply
  1. Krishna Pillai says:
    
    February 10, 2009 at 8:00 pm
    
    @mimo: Sorry, I have not studied the case where there is ISI plus MIMO. Most of my MIMO analysis was assuming flat fading. Kindly do share your results when they are available. Good luck
    
    Reply
Jarrod says:

November 29, 2008 at 11:52 pm

Thanks a lot for this blog. I am curious how your model of the Zero Forcing equilizer would differ if the channel was ISI instead of the MIMO?

Reply
Pingback: MIMO with ZF SIC and optimal ordering
Krishna Pillai says:

November 26, 2008 at 6:14 am

@lvs: Thanks :). This blog is my humble way of sharing what I know and hopefully learn more during the process.

I started off some time last year by writing posts on SER/BER computation of different modulation schemes in AWGN
https://dsplog.com/tag/awgn/

Later moved on to Rayleigh multipath channel model
https://dsplog.com/tag/Rayleigh/

Then started on receive diversity (EGC, MRC, selection combining) and transmit diversity (alamouti STBC)
https://dsplog.com/category/diversity/

And recently to MIMO
https://dsplog.com/tag/mimo/

Once in a while tries to discuss topics on negative frequency etc
https://dsplog.com/category/miscellaneous/

I sure do hope to make the contents more readable/friendly by putting some real world examples. Need to think of a way to fit in.

Btw, you have a really good blog out there. Nice long articles. I have bookmarked for future read.

Thanks.

Reply
lvs says:

November 23, 2008 at 9:25 pm

A DSP blog 🙂 Amazing, the internet does have it all!

A long time ago I used to work in DSP and communications. Since then this world has completely changed. I am looking forward to catching up by reading your blog.

You seem to have put a lot of effort, even have equations in here.

I have started out with this article so I dont know if I have missed some things…but you could make it more easier and interesting for readers like me through real life examples and putting more of your own insights into the equations.

Reply
Pingback: MIMO with Zero Forcing Successive Interference Cancellation equalizer
Pingback: MIMO with MMSE equalizer