This is the first post in the series discussing receiver diversity in a wireless link. Receiver diversity is a form of space diversity, where there are multiple antennas at the receiver. The presence of receiver diversity poses an interesting problem – how do we use ‘effectively‘ the information from all the antennas to demodulate the data. There are multiple ways to approach the problem. The three typical approaches to be discussed are – selection diversity, equal gain combining and maximal ratio combining. In this post we will discuss selection diversity. For the discussion, we will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
Background
1. We have N receive antennas and one transmit antenna.
2. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
3. The channel experienced by each receive antenna is randomly varying in time. For the receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
are Gaussian distributed having mean 0 and variance 1/2.
4. The channel experience by each receive antenna is independent from the channel experienced by other receive antennas.
5. On each receive antenna, the noise has the Gaussian probability density function with
with
and
.
The noise on each receive antenna is independent from the noise on the other receive antennas.
6. At each receive antenna, the channel is known at the receiver. For example, on the
receive antenna, equalization is performed at the receiver by dividing the received symbol
by the apriori known
i.e.
where
is the additive noise scaled by the channel coefficient.
7. In the presence of channel , the instantaneous bit energy to noise ratio at
receive antenna is
. For notational convenience, let us define,
.
From the discussion on chi-square random variable, we know that, if is a Rayleigh distributed random variable, then
is a chi-squared random variable with two degrees of freedom. The pdf of
is
.
What is selection diversity?
Consider a scenario where we have a single antenna for transmission and multiple antennas at the receiver (as shown in the figure below).
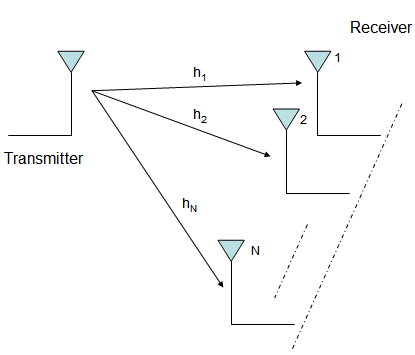
Figure: Receive diversity in a wireless link
At the receiver we have now N copies of the same transmitted symbol. Which then poses the problem – how to effectively combine them to reliably recover the data.
Selection diversity approach is one way out – With selection diversity, the receiver selects the antenna with the highest received signal power and ignore observations from the other antennas. The chosen receive antenna is one which gives .
Outage probability in Selection Diversity
The equations in the post refers the note on Receive diversity by Prof. RaviRaj Adve.
To analyze the bit error rate, let us first find the outage probability on the receive antenna. Outage probability is the probability that the bit energy to noise ratio falls below a threshold. The probability of outage on
receive antenna is,
.
is the defined threshold for bit energy to noise ratio.
In N reveive antenna case, the probability that all bit energy to noise ratio on all the receive antenna are below the threshold is,
,
where
are the bit energy to noise ratio on the 1st, 2nd and so on till the Nth receive antenna.
Since the channel on each antenna is assumed to independent, the joint probability is the product of individual probabilities.
.
Note that the equation above defines the probability that the effective bit energy to noise ratio with N receive antennas (lets call ) is lower than the threshold
. This is infact the cumulative distribuition function (CDF) of
. The probability density function (PDF) is then the deriviate of the CDF. 🙂
.
Given that we know the PDF of , the average output bit energy to noise ratio is,
.
This means that,
– with two receive antennas the effective bit energy to noise ratio is 1.5 times ,
– with three receive antennas, the effective bit energy to noise ratio is 1.833 times ,
– with four receive antennas, the effective bit energy to noise ratio is 2 times and so on.
If you recall the results from the AWGN with receive diversity case,
Effective bit energy to noise ratio in a N receive antenna case is N times the bit energy to noise ratio for single antenna case.
With selection diversity we are seeing that the effective SNR improvement is not a linear improvement with increasing the number of receive antennas. The returns diminish.
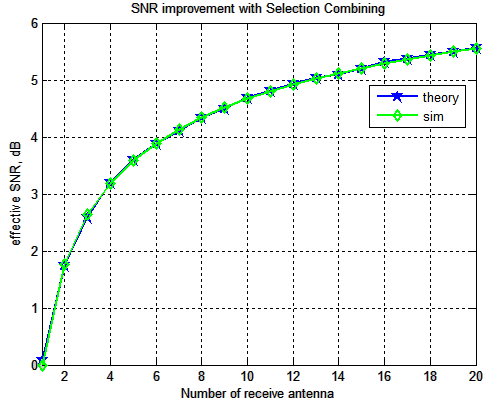
Figure: SNR gain with selection diversity
Click here to download Matlab/Octave script for computing the effective SNR in Ralyeigh channel with selection diversity
Bit Error probability with selection diversity
If you recall, in the post on BER computation in AWGN, with bit energy to noise ratio of , the bit error rate for BPSK in AWGN is derived as
.
Given that the effective bit energy to noise ratio with selection diversity is, the total bit error rate is the integral of the conditional BER integrated over all possible values of
.
.
This equation reduces to
.
BER Simulation Model
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Multiply the symbols with the channel and then add white Gaussian noise.
(c) At the receiver, find the receive path with maximum power
(d) Chose that receive path, equalize (divide) the received symbols with the known channel
(d) Perform hard decision decoding and count the bit errors
(e) Repeat for multiple values of and plot the simulation and theoretical results.
Click here to download Matlab/Octave script for simulating BER for BPSK in Rayleigh channel with selection diversity
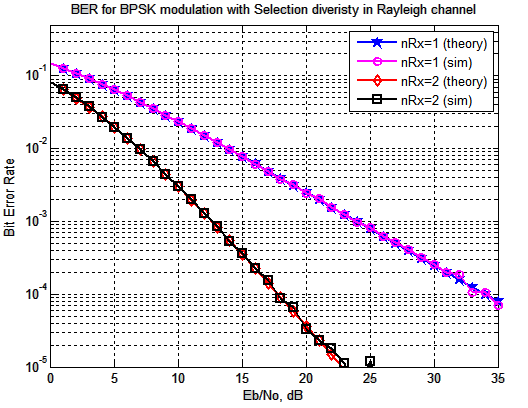
Figure: BER plot for BPSK in Rayleigh channel with Selection Diversity
Observations
Around 16dB improvement at BER point by with two receive antenna selection diversity 🙂
References
Receive diversity – Notes by Prof. Raviraj Adve
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
Happy learning.




Hi, sir . In selection diversity, You have calculated the effective snr as:
EbN0EffSim(ii,jj) = mean(hSel.*conj(hSel));
EbN0EffThoery(ii,jj) = sum(1./[1:nRx(jj)]);
But I think it should be
EbN0EffSim(ii,jj) = mean(ySel.*conj(ySel))/nRx(jj);
EbN0EffThoery(ii,jj) = (1 + (nRx(jj)-1)*pi/4);
If i am wrong please help me out and tell me the reason of using “hSel” instaed of “ySeal”.
Thank You.
@bhusan: The term ySel includes the effect of noise too. As I did not want to factor in the effect of noise, used hSel.
How is the pi/4 term coming?
Hi sir
are the receiving diversities (e.g MRC EGC) designed for SIMO system only? or it is used in MIMO system? I mean does the STBC decoder acts as receiving diversity?
@zeyad: A simple STBC decoder with 2 transmit antenna and 1 receive antenna. It is exploiting the diversity, but I reckon it would fall into the transmit diversity bucket.
Dear Sankar,
I have read some of your topics. It’s wonderful! It’s easy to understand for freshman.
There are two unsolved problems in this post. Maybe I can give you some advice.
1. the average output bit energy to noise ratio
The final result can be derived by using Mathematical induction [R1].
2. the total bit error rate
After expanding $[1-exp(-\gamma/(Eb/N0))]^{N-1}$ and with the aid of [R2, eq. (5A.2)], the final equation can be solved after some manipulations.
Good luck.
yangkai
[R1] http://en.wikipedia.org/wiki/Mathematical_induction
[R2] M. K. Simon and M.-S. Alouini, Digital Communication over Fading Channels—A Unified Approach to Performance Analysis
@yangakai: Thanks much. 🙂
Hi Sir,
Your posts have been so helpful to me. Thanks a lot.
I have a question,if have to combine selection diversity and Equal gain combining i.e SC2, what modifications have to be done?
I tried a lot, but my results seem to be wrong.
Please help.
@Soumya: Sorry, did not understand your question. Did you mean having the two set of results in the same plot?
I meant, if there are L branches, 2 branches with the best SNR(i.e second order selection combining) will be selected and combined using EGC…
Please Help..
@Soumya: Aah, am hoping that you will be able to adapt the existing matlab code(s) on Selection Diversity and Equal Gain Combining to meet your requirements.
https://dsplog.com/2008/09/06/receiver-diversity-selection-diversity/
https://dsplog.com/2008/09/19/equal-gain-combining/
hi sir, i tried a lot…but i am not able to find the second highest SNR properly..how do i do that?
Please guide me..
@Soumya: Find the received power on each antenna and sort them
Hi!
Will you please guide me on ‘How can we implement different diversity schemes like frequency, time, spatial diversity on Awgn and Rayleigh channel in case of BPSK and QPSK??’
Thanks..
@Navneet: Please look at
http://www.dsplog.com/tag/diversity
Hello Sir,
your site is really helpful…. I am doing my research in Turbo coded OFDM over frequency selective fading channels… I am using 1/2 and 1/3 rate turbo codes to reduce BER.. Could you help me on 1/3 rate turbo codes????
@Suchita: Sorry, I have not yet posted anything on Turbo codes
just wana say 4 all of ur topics..”simply awsm” . GOD BLESS U
Awesome Man that really helped me out, bookmarking you thank you so much 🙂
Dear krishna,
How could DPSK be implemented in Selection diversity? and how to be simulated?
thanks in advance
@Ahmed: Should be possible. I have not tried though
Dear krishna,
How could DPSK be implemented in Selection diversity?
thanks in advance
Please,Can you give me a matlab program for MxN MIMO OFDM system that transmitting independent data streams from each antenna (Spatial multiplexing)
@kimos_kh: I have not discussed the MxN MIMO OFDM case. However, you can find articles on 2×2 MIMO case at https://dsplog.com/tag/mimo
i have doubt in this program/
1) why same equation for the AWGN noise and Ray-laigth channel.
2) how can we find power using this equation: hPower = h.*conj(h);
please help me as soon as possible.
@vijayendra: My replies
1) Where did you see the same equation for AWGN and Rayleigh channel?
2) Assume h = a+jb. h*conj(h) = (a+jb)*(a-jb)= a^2+b^2 ==> power of h
Krishna Pillai,
Hellos sir,
I am told to assume Rayleigh fading channel with BPSK modulation. Using MATLAB
plot bit error probability (BEP) under coherent and non-coherent detection
when receiver is equipped with three antennas to exploit diversity.
Your figures will include plots from simulation. Use average SNR (complex)
from -5 to 20 dB.
Please help me resolve this, thank you so much
@Obinna O: Hope you have finished the project by now.
No sir,
I have not, I was awaiting your reply and assistance. I am still in need of your assistance.
@Obinna: Please take a look at
a) BER for BPSK in flat fading Rayleigh channel
https://dsplog.com/2008/08/10/ber-bpsk-rayleigh-channel/
b) BER for BPSK using selection diversity in flat fading Rayleigh channel (two rx antenna)
https://dsplog.com/2008/09/06/receiver-diversity-selection-diversity/
Thank you so much sir. It was very helpful
Hi Krishna,
Thanks for the well written post.
@Bhavesh: Thanks
Antenna selection can be implemented at both transmit and receive ends.
In Transmit antenna selection (TAS), Source has multiple antennas and receiver has single anenna, with the feedback information from the receiver to source, the single antenna will be selected for tranmission which has highet SNR.
The PDF and CDF of both schemes are same, so we can say that the perofrmance of both should be same.
For example
In SC, the receiver selects the largest SNR branch, i.e,
SNR_SC =max[h1, h2,… hk]
In TAS, through the feed back information from receiver to source, the source will select one of its antenna for transmission, which has highest SNR, i.e,
SNR_TAS=max[h1, h2,… hk]
So, only single channel will be seen by receiver from tranmit antennas amog all.
About PDF this defination is valid for both:
The probability density function of selecting the largest random variable amog k independent and identically random variables can be writen as:
PDF=k[ pdf of SNR of single channel]^k-1 *cdf of single channel
I think u can get my point now , further discussion will be welcomed
References:
[1] Shuping Chen, “Performance of Amplify-and-Forward MIMO Relay Channels with Transmit Antenna Selection and Maximal-Ratio Combining” 2009. WCNC 2009. IEEE
[2] Zhuo Chen , “Analysis of transmit antenna selection/ maximal-ratio combining in Rayleigh fading channels”, July 2005, IEEE
@Ayaz-korea: Thanks, I got you. Yes we select the best transmit antenna out of h1, h2, h3. So the final channel model is same in both transmit selection and receive selection. I agree with your comments.
According to my study, there is no difference in performance of Transmit Antenna Selection (at source) and Selection Diversity (at destination), wether by implementing the multiple antennas at source or destination, (like transmit beamforming and receive beamforming)
Are you agree with this??????
@Ayaz-korea: I did not quite understand, how you do the transmit selection? When we send from multiple transmit antennas, the new channel as seen by the single antenna receiver is
y = (h1+h2+h3)x + n, where
h1, h2, h3 are channel seen by the receiver from transmit antenna 1, 2, 3 respectively.
Agree?
In this case, how do we do the selection?
could you please explain : how you have model white Gaussian noise as a two random variables multiblyed by Eb/No ??
as you have given Rayliey noise the code ( h) and white Gaussian noise ( n) while they are both the same .
do you have a referenc you have based on in your model
@Ayhem: This concept is discussed in most text books on digital communications. You may refer Digital Communications by John Proakis.
Wiki references:
http://en.wikipedia.org/wiki/Johnson%E2%80%93Nyquist_noise
http://en.wikipedia.org/wiki/Rayleigh_fading
May I know what type of real life applications uses simo? Is handphone (1 antenna) to base station (many antenna) 1 of the application?
@bluray: Yes, uplink communication (handphone-to-basestation) is a valid application. However, in future, we might be seeing handphones with multiple antennas 🙂
what is different symbol eeror rate with bit error rate
@wayan: By symbol, we typically refer to the constellation symbol as defined by the modulation scheme like BPSK, QPSK, 16QAM, 16-PSK etc. By symbol error rate, we count the number of errors where the received constellation symbol differs from the transmitted constellation.
Each constellation symbol may correspond to a group of bits. So, each symbol error may constitute one or more bit errors.
The post on BER with 16-QAM should be helpful to understand the concept
https://dsplog.com/2008/06/05/16qam-bit-error-gray-mapping/
Good luck.
hello khrisna how to diversity selection in riciab fading channel…pleasee
@lila: I have not tried modeling in Rician fading channel. However, I would think that the concept remains the same – chose the path with higher signal to noise ratio
Thank you for all your posts. No other way is easier to start matlab in wireless communication as effective as reading your posts.
I wish you all the best, and hope that ultimate coding techniques will be discussed further such as: LDPC, Turbo Coding,…
@Mr.Bean: Thanks, kind words indeed.
Sure, I do hope to move on to LDPC, Turbo decoding etc (as soon as I learn them)…;)
@Mr.Bean: Thanks, kind words indeed.
Sure, I do hope to move on to LDPC, Turbo decoding etc (as soon as I learn them)…;)
how to reliase selection combination with QAM-16 modulation…please help me sir
@debabandana: I think it should be reasonably easy for you to adapt the code in this post Selection diversity with BPSK to 16-QAM case. For BER/SER with 16-QAM, you may look @
(a) https://dsplog.com/2007/12/09/symbol-error-rate-for-16-qam/
(b) https://dsplog.com/2008/06/05/16qam-bit-error-gray-mapping/
Hope this helps
hi,,
i want to know and i need help about BER for QPSK in rayleigh and rician fading channel with selection diversity,,would you please explain to me..
@well: This post discuss BER for BPSK in Rayleigh channel with selection diversity. I would think it would be reasonably easy to adapt to QPSK case.
I have not tried modeling Rician channel. Plan to do so in future.
Can you help me about SIR based selection diversity script?
How to implement these schemes with Nakagami-m and alfa-mu fading distribution?
@Stefan: I have not tried modeling the Nakagami-m or alfa-mu fading model. You may use,
http://en.wikipedia.org/wiki/Nakagami_distribution
I would think that the selection algorithm still remains the same. Its only the noise and channel model which changes.
Can you tell me how to implement these schemes with Rician fading distribution?
@Bhumika: I think the algorithm for doing the selection diversity still remains the same. It is the channel model which changes from Rayleigh to Rician. I have not studied the modeling of Rician channel.