(15 votes, average: 4.07 out of 5)
Loading ...
Mr. Lealem Tamirat, in a comment on BER for BPSK in Rayleigh channel, wondered about the performance of an OFDM modulated system in a frequency selective Rayeligh fading channel. My response was that,
Though the total channel is a frequency selective channel, the channel experienced by each subcarrier in an OFDM system is a flat fading channel with each subcarrier experiencing independent Rayleigh fading.
So, assuming that the number of taps in the channel is lower than the cyclic prefix duration (which ensures that there is no inter symbol interference), the BER for BPSK with OFDM in a Rayleigh fading channel should be same as the result obtained for BER for BPSK in Rayleigh fading channel.
Let us try to define a quick simulation to confirm the claim.
OFDM system
Let us use an OFDM system loosely based on IEEE 802.11a specifications.
| Parameter | Value |
| FFT size. nFFT | 64 |
| Number of used subcarriers. nDSC | 52 |
| FFT Sampling frequency | 20MHz |
| Subcarrier spacing | 312.5kHz |
| Used subcarrier index | {-26 to -1, +1 to +26} |
| Cylcic prefix duration, Tcp | 0.8us |
| Data symbol duration, Td | 3.2us |
| Total Symbol duration, Ts | 4us |
You may refer to post Understanding an OFDM Transmission and the post BPSK BER with OFDM modulation for getting a better understanding of the above mentioned parameters.
Eb/No and Es/No in OFDM
The relation between symbol energy and the bit energy is as follows:
.
Expressing in decibels,
.
Rayleigh multipath channel model
As defined in the post on Rayleigh multipath channel model, the channel was modelled as n-tap channel with each the real and imaginary part of each tap being an independent Gaussian random variable. The impulse response is,
,
where
is the channel coefficient of the 1st tap,
is the channel coefficient of the 2nd tap and so on.
The real and imaginary part of each tap is an independent Gaussian random variable with mean 0 and variance 1/2.
The term is for normalizing the average channel power over multiple channel realizations to 1.
Figure: Impulse response of a multipath channel
Cyclic prefix
In the post on Cyclic Prefix in OFDM, we discussed the need for cyclic prefix and how it plays the role of a buffer region where delayed information from the previous symbols can get stored. Further, since addition of sinusoidal with a delayed version of the sinusoidal does not change the frequency of the sinusoidal (affects only the amplitude and phase), the orthogonality across subcarriers is not lost even in presence of multipath.
Since the defined cyclic prefix duration is 0.8us duration (16 samples at 20MHz), the Rayleigh channel is chosen to be of duration 0.5us (10 taps).
Expected Bit Error Rate
From the post on BER for BPSK in Rayleigh channel, the BER for BPSK in a Rayleigh fading channel is defined as
.
I recall reading that Fourier transform of a Gaussian random variable is still has a Gaussian distribution. So, I am expecting that the frequency response of a complex Gaussian random variable (a.k.a Rayleigh fading channel) will be still be independent complex Gaussian random variable over all the frequencies.
Note: I will update the post, once I am able to locate the proof for “frequency response of a complex Gaussian random variable is also complex Gaussian (and is independent with frequency)“.Given so, the bit error error probability which we have derived for BER for BPSK in Rayleigh channel holds good even in the case of OFDM.
Simulation model
Click here to download: Matlab/Octave script for BER simulation of BPSK in a 10-tap Rayleigh fading channel
The attached Matlab/Octave simulation script performs the following:
(a) Generation of random binary sequence
(b) BPSK modulation i.e bit 0 represented as -1 and bit 1 represented as +1
(c) Assigning to multiple OFDM symbols where data subcarriers from -26 to -1 and +1 to +26 are used, adding cyclic prefix,
(d) Convolving each OFDM symbol with a 10-tap Rayleigh fading channel. The fading on each symbol is independent. The frequency response of fading channel on each symbol is computed and stored.
(e) Concatenation of multiple symbols to form a long transmit sequence
(f) Adding White Gaussian Noise
(g) Grouping the received vector into multiple symbols, removing cyclic prefix
(h) Converting the time domain received symbol into frequency domain
(i) Dividing the received symbol with the known frequency response of the channel
(j) Taking the desired subcarriers
(k) Demodulation and conversion to bits
(l) Counting the number of bit errors
(m) Repeating for multiple values of Eb/No
The simulation results are as shown in the plot below.
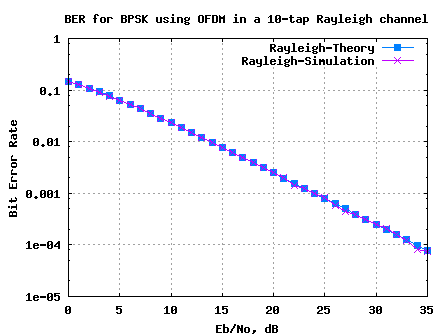
Figure: BER plot for BPSK with OFDM modulation in a 10-tap Rayleigh fading channel
Summary
1. The simulated BER results are in good agreement with the theoretical BER results.
2. Need to find the proof for frequency response of a complex Gaussian random variable is also complex Gaussian (and is independent with frequency).
Hope this helps. Happy learning.
Related posts
- Cylcic prefix in Orthogonal Frequency Division Multiplexing
- Rayleigh multipath channel model
- BPSK BER with OFDM modulation
- BER for BPSK in Rayleigh channel
- BER for BPSK in ISI channel with Zero Forcing equalization
D id you like this article? Make sure that you do not miss a new article by subscribing to RSS feed OR subscribing to e-mail newsletter. Note: Subscribing via e-mail entitles you to download the free e-Book on BER of BPSK/QPSK/16QAM/16PSK in AWGN.
{ 225 comments… read them below or add one }
Thank you!!! Krishna ur script helps me very much for my work. i am trying to simulate performance of adaptive OFDM as per current conditions of the wireless channel. if i am going to face a problem i will try to inform you.
Thank you!!!!
Hello Dear Mr Krishna
thanks for your comprehensive posts
could you please explain that:
1 – if the channel is slow fading
how can we apply the correlation between the channel coefficients for several ofdm symbols depending on the coherence time of the channel
2 – how can we estimate the channel coefficients in this scheme when we apply the block type pilot channel estimation
and at last
3 – could you please show how should we equalize the received signal with MRC scheme
I have some problems in writting matlab program so could you please guide me by that
best regards
@ mohamadali:
1. I would think that, if one knows the way the channel will evolve (second order statistics like autocorrelation etc), then one could define a set of coefficients which can be used to obtained averaged estimates. However, since I have not tried out this, I am unable to comment well on this now.
Further, similar to time domain correlation, one may also use the frequency domain correlation i.e. if the evolution of channel on the frequency domain is known, use to obtain a better estimate of the channel.
2. Apart from the block pilots, which provides the initial estimate, one may have pilot subcarriers in the data symbols. However, we need to have quite-a-bit of pilot subcarriers to ensure that we can do the interpolation across subcarriers well.
Another way, if the SNR is good, is to use hard-decision decoding and use the hard decision as the reference symbol.
3. MRC – maximal ratio combining ensures that information on both the dimensions is optimally combined to demodulate the symbol. I will write a post on the same soon.
Thanks Dear Krishna
Will you have a matlab program on estimating the slow fading channel coefficients for ofdm systems in the near future based on block pilot aided channel est. on your blog
and will you work on space-time Tx diversity for OFDM or MC_CDMA system
I am simulating a mc-cdma system and i faced with these problems:
if you let me I send you my matlab code, if it is possible for you please guide me:
1.I used the channel coefficients were produced by the method that linnartz presented in his site based on generation of coefficient for each subcarrier in frequency domain since the channel will be narrowband for each subcarrier after ofdm modulation with assuming jakes psd.
I dont know how should will be treat in this approach with generated signal and channel(should we directly multiply the two same length Txed signal and channel or not) and how should we extract channel coefficients after getting fft from Rxed signal (in time domain we got fft from the channel coefficients )equalize the received signal by various equalizing scheme such as MMSE,LS,MRC,ORC
2. according to my code how can i make the correlation between two ofdm symbols based on slow fading channel properties
and at last if you know any helpful matlab program on simulation of MC-CDMA systems please tell me because i am new with this kind of systems and despite my studying papers
i confused in some simulating points.
Thanks
@mohamadali:
I plan to add contents on
(a) slow fading channels in OFDM (as used in 802.11a WLAN system)
(b) Tx diversity schemes like Alamouti coding, cyclic shift diversity etc
1. Though am not familiar with the Linnartz paper, yes you can assume that the channel is flat fading for each subcarrier. You can convolve the channel with the transmit sequence. If frequency, it will be multiplication if the channel response duration is less than the cyclic prefix.
2. As stated prior, I have not worked well on exploiting the correlation thing. Will do in future.
You can ask specific questions on MC-CDMA. Having a good understanding of OFDM should help you get going.
Hi krishna..
Your simulation is great but i have a question.
For this thing to get work on some hardware the transmitted real and imaginary part should be within the range of +1 and -1. But with the normalization factor that you have introduced i.e. nFFT/sqrt(nDSC) with IFFT in the code, the transmitted real and imaginary amplitudes go way beyond +1 and -1. (Assuming Q1.15 format). What do you think should be appropriate scaling factor.
Best Regards
@noamchomsky (really???)
It seems that you are looking for fixed point conversion i.e to represent the numbers as integers. One way to do this would be to
(a) convert the signal into the range of -1 to +1 by
dividing by the maximum of the absolute value from the real part or imaginary part.
(b) Convert to an integer by multiplying and 2^n and rounding.
i.e if xt is the signal
N = 10; number of bits (signed number)
xt_scaled = xt/max(max(abs(real(xt))),max(abs(imag(xt))));
xt_fixed = round(xt_scaled*2^(N-1));
Did this help?
Well thanks for your prompt reply krishna… But my question is still there.
When we are transmitting the signal we cannot scale it by dividing the maximum value. In this case, the scaling factor would be different each time we transmit the signal depending upon the PAPR (peak to average power ratio) of the signal. What i wanted to know is that what is the appropriate scaling factor used in this case that bounds the signal values within +1 and -1. Or if industry uses the same divide-by-maximum-value algorithm, am i wrong in the claim above.
Best Regards,
@noamchomsky:
With the industry case, things are a bit different, but the same concept holds good.
For the OFDM case, till the input of QAM mapping, the representation will be in bits (1bit). At the QAM mapping o/p, we represent the complex number into fixed point arithmetic represented in N bits. The value of N is a tradeoff between the hardware constraints and accuracy. Higher N means more accurate, but requires more hardware.
This complex o/p of QAM mapping is followed by a fixed point ifft(), filters and so on.
Hi Krishna,
Your website is a life saver. thanks
Question: in your code for this section , you are undoing the affect of the channel with following line:
% equalization by the known channel frequency response
yF = yF./hF;
I am sure I am missing some theoretical concept here. However if you undo the affect of the channel before slicing and demodulation , then what is the purpose of the channel filter.
appreciate a response.
jamal
@jamal: By channel filtering, I think you are referring to the inverse filtering operation such that h(t) * c(t) = delta(t), where
h(t) – is the channel impulse response
c(t) – is the channel equalization filter
* – is the convolution operator and
delta(t) – is the impulse
Am I correct?
Note that in OFDM, the channel response becomes a single tap filter – such that convoltion becomes just a multiplication. So to undo the effect of multiplication, we divide by the known channel. Does that make sense?
Thanks Krishna.
The purpose of using a filter(h(t)) is to simulate the affect of a signal going through a real life channel. This real life channel impairments translates to the BER curve.
So by undoing the response by a known channel frequency response. How is the BER now relates to the 10tap filter that it went through. You just removed the affect of the channel before you went into your receiver function.
Yes I do understand that equalization in OFDM occurs in frequency domain , hence a divide. So an essence OFDM system can not function with out a fairly accurate channel estimation .
thanks for helping me out. DSP can be a black magic at times.
best regards
Jamal
hi,
sorry if this sounds like a stupid question
im rather new in this..
if the BER shows no improvement in Rayleigh fading channel, why do we perform this simulation??
@ila: No, not a stupid question at all.
At the least, we should know that the BER does not degrade with OFDM.
In general, I felt some readers might feel comfortable having a OFDM + multipath simulation. Hence tried to characterize the performance.
@ila: Raleigh represent wireless channel under certain limitation. Were awg is basically noise, you could assume point to point link with no Multipath.
Therefore to see the performance of OFDM ,one has to run the simulation with and without Cyclic prefix. Krishna simulation is set up to make those changes. what you can do is to progressively increase the delay spread and see the simulation degrade.
Well jamal the reason why this channel inversion will have an effect on this simulation is because it will increase the noise in the case where there is a fade in any subcarrier. For example, consider y as the output at any subcarrier
y = x + n ;
where x is the data value and n is noise
when you invert the channel,
y/h = x/h + n/h;
the noise is scaled accordingly.
In case, when there is a deep fade at any subcarrier, the channel estimation will try to increase x as much as possible and will increase the noise accordingly. That’s why we cannot say that this channel inversion combined with channel filtering has no effect on the performance.
I hope this answers your query..
dear krishan , thanks very much a bout your excellent efforts, but i have some questions a boout rayleigh with ofdm.
1-what is the no. of rayleigh paths and their average gain.
2-what is the max. doppler shift.
3-what is the channel coding used.
4-what is the delay spread.
5-can you, kindly give us ofdm simulation with differnet modulations types such as(QPSK,16QAM) and their scripts.
6-through my reading, i find (rayleigh flat fading) what is mean ,and is flat mean we have one path.
with my best regards
tariq
@tariq: Please find my responses below:
1. 10 tap channel with average gain of unity.
2. No doppler is simulated
3. No channel coding
4. I have not computed the delay spread, but should be reasonably easy to compute given that we know the number of taps and their gain.
5. you have the model with BPSK. It should be reasonably easy to extend it to QPSK/QAM cases.
6. In OFDM case, though rayleigh channel has multiple taps, for each subcarrier the channel is effectively a single tap channel. Hence frequency selective fading channel becomes a flat fading channel with ofdm.
Hope this helps.
Hi Krishma,
When I try to extend to QPSK, I meet the problems on demodulation part. Seems that the BER increse dramatically.
The method I do is fist mapping the 0,1 bit to QPSK signal, which is 1+j,1-j,-1+j,-1-j. And take this symbols into the IFFT and FFT calculation.
What would be the problem??
THX!
@Ray: hmm… well extending to QPSK should be reasonably simple. Maybe the first approach is to make sure that symbol error rate with QPSK is computed correctly. Once that simulation is stable, one may proceed to map the constellation symbols to bits and find the BER.
The following post maybe useful:
http://www.dsplog.com/2007/11/06/symbol-error-rate-for-4-qam/
HI Mr.CHRISHNA..
REGARDING UR POSTS UPWARD,HOPE U HELP ME FIGURING OUT THIS PROB FACING ME LONG TIME AGO:
AM SIMULATING AN OFDM SYSTEM IN THE FRONT-END IN THE Rx SIDE IN ORDER TO ESTIMATE THE MAX PEAK OF PILOT ISERTING IN THE DATA SEQUENCE IN THE Tx SIDE,BY USING AUTO-CORRELATION IN TIME DOMAIN(BEFORE FFT)..FOR THE AWGN CHANNEL I GET QUITE GOOD RESULS..BUT THE PROBLEM TAKES PLACE WHEN TRYING THE RAYLEIGH FADING CHANNEL..
PLEASE TRY TO HELP HIM AS MUCH AS U CAN..
ANY MORE DECLARATION PLS WRITE TO ME AT gafer2306 AT gmail.com
THANX ALOT.
@GRS: What is periodicity of the preamble of the transmit sequence. If the multipath channel is of lower duration than the periodicity, then I do not think auto-correlation o/p should be affected by the multipath channel.
Thanx for replying Mr.Krishna..
In fact it isn’t a pure preamble,i mean,not a separate sequence transmitted periodically,but,instead,it’s a kind of PSAM system..Pilot Symbol Assisted Modulation..That is:
* The pilots are inserted along with the data sequence periodically,means after every certain amount of data-subcarriers there will be a pilot subcarrier..e.g.every ten,the eleventh is a pilot.
* We’ve 100 pilots per a symbol,say..means,1100 data subcarriers..1200 subcarriers (samples) per symbol.with a duration of 120us..say.
* The cyclic prefix is 1/4..30us.
* we locally regenerate the pilot in the Rx with duration and POWER LEVEL (AMPLITUDE) as same in the Tx side but before the transmission (before the channel).
* We are concerning the POWER LEVEL of the pilots and need to estimate it by using auto-correlation in the Rx’s front-end.
***For AWGN we’ve simply discarded the cyclic prefix..and directly do auto-corr between the received signal and the locally generated pilot sequence,,and we get somehow reasonable estimated peak for the pilot..as well as the index (delay).
*** By the way, am using Simulink.
*** Hope it is clear for u..but any more or deep details needed am here..really waiting for help.
Thanx again.
Hi again Mr.Krishna..
Another basic question Sir..What is the difference between the number of channel Taps and the number of Rays?? What i get from somewhere that ONE Tap is consist of a GROUP of RAYS..is it correct?? If so,How can I determine that number of Rays for each (ONE) Tap?? Depending one what I mean..Time delay profile??((This is in case of multipath channels..As Rayleigh))As U know!!
@GRS: On your first question on pilots
As I understand from you, you have pilots subcarriers embedded in your data subcarriers in the OFDM symbol. How are you planning to use the pilots?
As I can recall, typically for systems like 802.11a, the pilots are used to track the residual carrier frequency offset error, sampling clock offset error etc. There we find the phase of the received pilots given that we know what was transmitted, and uses the phase information from multiple pilot values to form the estimate.
I do not understand the expectation from your side when you say – “you do autocorrelation of the pilot sequence”.
Can you please point me to the paper which you are refering to for the algorithm.
Hi again after long time Mr.krishna..
1) Well,forget about the pilot for now.
2) Am focusing only on the time-doman signal..before the fft.
3) Simply , by using the auto-correlation (of the received signal with it self) i manage to estimate the received average power..without any delay this corresponds to the zero-lag peak..with the AWGN this can work,but for the RAYLEIGH the problem takes place.
The question again is like this:
How could I estimate the channel (in order to componsate for it) in the case of time-domain..not in the frequency-domain???
@GRS: My replies
1/ ok
2/ ok
3/ ok, i understood how you are estimating the power.
I can think of one way of estimating the channel in time domain. Let us say you have a known preamble in time domain, p(t).
Also, let the preamble has
a) good cross-correlation properties i.e p(t) * p(-t) = impulse, d(t)
b) and does not correlate with noise i.e n(t) * p(t) = 0
where * is the convolve operator
The received signal is
y(t) = c(t) * h(t) + n(t)
Convolve the received signal with the time-reversed complex conjugate of the known channel i.e
m(t) = y(t) * p(-t) = c(t) * h(t) * p(-t) + n(t) * p(-t)
Since c(t) * p(-t) = d(t) and n(t) * p(-t) ~= 0, we have
m(t) = h(t)
Does this help?
Yaa Thanx..but:
1) Whats the difference between p(-t) here,when u said:”Also, let the preamble has
a) good cross-correlation properties i.e p(t) * p(-t) = impulse, d(t)” and when u said:”Convolve the received signal with the time-reversed complex conjugate of the known channel i.e
m(t) = y(t) * p(-t)”????
2)”Since c(t) * p(-t) = d(t) and n(t) * p(-t) ~= 0, we have
m(t) = h(t)” … I think u mean: m(t) = h(t)d(t).. right?
3)After estimating this h(t), how could I compensate for it? Is it just multiplying of the received signal by the inverse of the estimated channel..[1/h(t)]??as the frequency domain equalization???
Thanx again.
cos in 1) above..I understood that in both cases we just do a cross-correlation..here:
((((a) good cross-correlation properties i.e p(t) * p(-t) )))) for the known channel with it self(auto-correlation)..
whereas here (((Convolve the received signal with the time-reversed complex conjugate of the known channel i.e
m(t) = y(t) * p(-t)))) cross-correlating the known channel with the received signal..
So my question in other words : Why did u say:
“Convolve the received signal with the time-reversed complex conjugate of the known channel i.e
m(t) = y(t) * p(-t)”
instead of just:
“cross-correlate the received signal with known channel”..whats the difference????
@GRS: My replies:
1/ Did not get your question. Difference between p(-t) and ?
2/ Yes, i mean m(t) = h(t) delta(t). Since delta(t) is impulse, I did not mention this explicitly.
3/ If the channel is not flat fading, then we need to find a new filter c(t), which undoes the effect of the channel, i.e h(t) * c(t) = delta(t)
@GRS: As I understand from Rayleigh multipath channel model
( http://www.dsplog.com/2008/07/14/rayleigh-multipath-channel/ ), each tap corresponds to a path having delay of tau(n) and amplitude of alpha(n).
I do not quite follow the term ray. Can you please point me to a paper please.
Hi Mr.Krishna..
regarding ur post above,,u mentioned that:
((I recall reading that Fourier transform of a Gaussian random variable is still has a Gaussian distribution. So, I am expecting that the frequency response of a complex Gaussian random variable (a.k.a Rayleigh fading channel) will be still be independent complex Gaussian random variable over all the frequencies.))
so hope u get that prove..I may strongly need it..hpoe u point me to the exact reference aloso..
thanx in advance.
respected sir,
I m btech final year student can u help me by giving me advice how to calculate “BER of OFDM on frequency selective nakagami-m fading channel”.Or if possible can u provide me matlab code for simulation.Any help in this regards will be benifical for me.
Thanking you
sahil chaudhary
dear Krishna,
I took several of your simulations and add channel coding (poly2trellis(3,[5 7])). I got the coding gains expected. Similar I get coding gain in your BPSK in OFDM with Rayleigh multipath channel simulation with ntap=10. But when I use channel coding in OFDM flat fading channel (ntap=1) I don’t get any coding gain. Curve is the same as OFDM uncoded. do you have any insights why this? I know i will get more coding gain in a frequency-selective channel but I will also expect some coding gain in a flat-fading channel, correct?.
keep with the good work.
@sahil: I have not done modeling of Nakagami fading channel, hence do not have code/results on the same. Hope the following
link is helpful.
http://wireless.per.nl/reference/chaptr03/ricenaka/nakagami.htm
@karl: Yeah, I would also expect to get coding gain with OFDM in AWGN channel. Did you try with simple AWGN channel alone (no OFDM)?
OR is it due to some scaling error in bit to noise ratio (Eb/No) vs code bit to noise ratio (Ec/No) vs SNR?
Please do report your findings. All the best.
Sorry sir this link doesnt help me lot.Can u provide me any information from where else i can get material to simulate nakagami-m fading channel.
thanking you
sahil chaudhary
Sir if you can provide me code for rician fading that would also help me a lot
Thanks
sahil
Sir if you can provide me code for calculating BER in rician fading that would also help me a lot
Thanks
sahil
@sahil : Sorry, I have not written any post on modeling Rician channel.
Hi Krishna..
[[[[[Comment by Krishna Pillai on November 26, 2008 @ 6:03 am
@GRS: On your first question on pilots
As I understand from you, you have pilots subcarriers embedded in your data subcarriers in the OFDM symbol. How are you planning to use the pilots?
As I can recall, typically for systems like 802.11a, the pilots are used to track the residual carrier frequency offset error, sampling clock offset error etc. There we find the phase of the received pilots given that we know what was transmitted, and uses the phase information from multiple pilot values to form the estimate.
I do not understand the expectation from your side when you say - “you do autocorrelation of the pilot sequence”.
Can you please point me to the paper which you are refering to for the algorithm.
]]]]]
sorry for late in replaying.
http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=1556874&isnumber=33117
((In this paper : only the magnitude of received signal is
used to obtain the time position of the pilot symbols))
We also need to estimate the magnitude of the received signal as well as pilots but for another issue than timing as mentioned earlier in my 2nd post.
Thanx.
for the second part i will point u 2 a paper.
hi mr pillai
in your code
xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xF.’)).’;
the power of each row becomes 64 and the norm of it becomes 8
should not we multiply ifft(fftshift(xF.’)).’ by
sqrt(nFFT/nDSC) instead (nFFT/sqrt(nDSC)) and in this condition the norm of each row will become 1 and so the power of each row will become 1 too.
@mohamadali: I just checked. The scaling by sqrt(nFFT/NDSC) ensures that mean power for each row becomes one i.e E{|xt|^2} = 1. Infact, I should have said mean power.
Does that help?
Dear Krishna
I am bit confused here. You said “The scaling by sqrt(nFFT/NDSC) ensures that mean power …” is it scaling by sqrt(nFFT/NDSC) or nFFT/sqrt(NDSC).
Kind Regards
A Mehboob
I need the matlab OFDM script in different channel.
@karim: which channel?
Hi ! I am a student of B.Sc. (Honors) Computer Science & Engineering in STAMFORD UNIVERSITY BANGLADESH . For my thesis i choose topics OFDDM( my work make OFDM CODE which use BPSK,QPSK and 16 QAM as OFDM modulation technique than code find which technique can efficient , fast, and low bit error etc)
Here any body help me about this,, plz mail me at: solimanhossain@yahoo.com.
Hello Krishna, I was going through simulation of BER for coherent Psk schemes with non-coherent PSk i.e. Differential PSK so DPSK of any modulation level was behaving much better than a coherent PSK. So my question is that why haven’t we seen more implementation of DPSK as compared to say GMSK, pi/4-QPSK or O-QPSK
Is there some problem of implementation, if so what is it?
I hope you’ll reply soon!
TC
@communications_engineer: Well, I do not quite understand why you are saying the Differential PSK was behaving much better than coherent PSK. Typically if we do non-coherent demodulation of DBPSK, then BER is expected to be around 3dB worse. Even if we do coherent demodulation of DBPSK, then the BER is double. I have written a post on coherent demodulation with DBPSK at
http://www.dsplog.com/2007/09/30/coherent-demodulation-of-dbpsk/
Hope that provides you some clues. Kindly do share your findings.
Krishna, I created an m-file to find the level crossing rate and the average fade time duration. First I found the BER for QPSK and for the same same of channel conditions I found for DQPSK.
Now the error rate under Rayleigh conditions (ts = 1e-3, fd=25) I received about 55% bits in error. However when I used DQPSK I had a BER of 25% which is significant difference. Also I later put an interleaver of depth 10 (depth suggested by AFTD) so in QPSK my BER reduced to 30% while for DQPSK my error was 3% Huge difference, right?
Your post finds the BER under AWGN where phase fluctuations are not severe unlike Rayleigh fading, try it using scatterplot in Matlab. So, I again repeat my question, DQPSK gives better results than QPSK under fading conditions so why is it not used in standards? Why is QPSK still prefered? Also with DQPSK we wont need a complex phase detector, right?
@communication: So your observation is that DQPSK gives better performance than QPSK in Rayleigh channel. Intetresting! May I ask one question: Do you have an equalizer in the receiver in your simulations?
No. No equalizer used
I wasn’t surprised. Look for BPSK we need have coherent demodulation. In AWGN that may be easy to have. However, in Rayleigh fading, the channel phase response changes dramatically. Now have a coherent demodulation will always produce bad results as phase is no longer preserved (I’m talking about fast and not slow fading). So with DBPSK (I’ve tested it on DBPSK and DQPSK) we can local, ‘differential’ synchronization. So even if channel phase response varies in what ever form it can, the performance does not get too worse. But you would already know that, right?
I also have an observation about convolutional encoder, but I’ll ask it on its page. You can contact me on my email address
@Communication: Good, so are in agreement. Since your receiver did not have equalization the DBPSK provided better performance. In typical systems, we do expect to have the equalizer in the receiver.
Hello Krishna
If I use an equalizer than the performance of DBPSK will also improve. Its not like BPSK improving 10 times and DBPSK 1 time.
But now I have found an answer to my question, why DBPSK is not commonly used in mobile communication
It would be good if you can simulate some of these topics in Simulink
@Communications: Can you please share your observation on “why DBPSK is not commonly used in mobile communication” in some more detail.
Well even though DPSK for M=2 or 4 are spectrally efficient, we STILL have those transition of phases through the center which makes the need for highly linear amplifiers, making the device based on this technique expensive. Thats the whole reason for using pi/4-QPSK, O-QPSK and GMSK, right? The so-called CPM
Acha Krishna have you considered Matlab/Simulink simulations for CDMA and IDMA. I would be interested in those. Especially in Simulink environment. I’m sure other people would too. May be allow other people to contribute as well, turn this into something like dsprelated.com
Krishna, you stated before that using a 10-tap channel, which is lower than the CP duration, BER for BPSK and BER for BPSK-OFDM will be the same, my question is what results are to expect for a channel with more number of taps e.g. 20 taps??
What would be the interpretation of that kind of channel and those results?
@Jose: I would think that the performance will be poorer due to the ISI caused by channel.
Good evening Mr. Krishna Pillal,
I fully respect your work!
I have carried wideband measurement campaign to measure the frequency response of a channel, it s length is 10,000 points. I need to investigate OFDM transmission using your OFDM code. my question to you is:
instead of using the rayleigh fading model in the code, is it correct to transform my measured frequency response to impulse response (IFFT(FR)=IR) then convolute this IR with the symbols then add noise and so on? note that the IR is almost 40 multipath components.
or is it possible to slice the FR and use it without converting it to IR.
I would be very greatful if you kindly provide me with some hints and the steps to follow.
my regards o you!
@Marwan: In the physical medium, the signal is getting convoluted with impulse response of the channel. In OFDM, if the cyclic prefix is more than the channel duration, you can alternatively model the effect of channel my multplication in frequency domain.
Hope this helps.
Hi Krishna,I think you can ignore my previous question,
I alresdfy convoluted my measured channel impulse response with the appended signal xt in time domaine:
but how the cyclic prefix is chosen on line 38 from[49:64], I know that 64 is the fft size, but why 49?
also in line 64, yt = yt(:,[17:80]);
after convolution the length of the signal become 89, the 89-(nTap-1)=80, but what is the 17 stands for?
Sorry! please, ignore my questions, i found answers.
Hi krishna,
I’d appreciate very much your patience! my question is:
in OFDM model, BER curve should coincide with theoretical ones at all times?. and by the way are you going to equalize in OFDM model using MMSE? I could not succeed in equalization using mmse method.
@Marwan: As the OFDM makes a multipath channel effectively a flat fading channel on each subcarrier, the BER performance with OFDM should be comparable to flat fading Rayleigh channel performance.
In the code, am equalizing by zero forcing. You need not use MMSE here. As I see, since there is no interference, the ZF equalization is optimal from BER perspective.
Hope this helps.
In your channel model the spacing between taps is constant (equally spaced taps), I guess the spacing between taps explains the delay arrival of each path on the multipath channel.
Is it always equally spaced taps which describes the multipath effect?
What would be a justification for using equally spaced taps on the simulation?
@Joe: Equally spaced taps need not be the case always. Atleast, for this simulations, the objective was to show that in OFDM, even with a multipath channel, the BER is same as in flat fading rayleigh channel.
In practise, the channel power delay profile maybe exponentially decaying (like Naftali model)
http://www.commsdesign.com/article/printableArticle.jhtml?articleID=16505977
Then there are channel models (like JTC), which specify channel taps without having equally spaced delay.
Hope this helps.
hello guys…..im doing my final year project of bachelors Regarding OFDM on simulink…uptill now i have done with IEEE802.11a OFDM with AWGN channels…now i have to extend it for MULTIPATH RAYLEIGH CHANNEL and EQUALIZERS…but im unable to proceed because when i insert rayleigh channel in place of AWGN in the model of 54Mbps…it gives an error of memory…and when i insert equaliser than it gives an error that input must be a complex vector at its input port….i dont know how to convert my input binary signal which is already in the form of double to Complex in order to make it compatible with Equaliser:(
PLZ SOMEBODY HELP ME…IS THERE ANY SIMULINK EXPERT HERE WHO HIMSELF OR HERSELF HAS WORKED ON MULTIPATH AND EQUALIZERS IN SIMULINK….IM RUNNING SHORT OF TIME…PLZZ MAIL ME IF U GUYS HAVE SIMULINK MODEL OF IEEE802.11a REGARDING MULTIPATH and EQUALIZER TO CORPORATE ISI….IT WILL BE OF GREAT HELP 4 ME…
MY EMAIL ADDRESS IS
zain.87@hotmail.com
will wait for response….plzzzzzzzzz HELP ME OUT
REGARDS
ZAIN
@zain: I do not have simulink with me, but I can point you to a post on BER for BPSK with OFDM modulation in Rayliegh channel.
http://www.dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
Further, in Mathworks website, there is 802.11a model (i think for AWGN only) in Simulink
http://www.mathworks.com/matlabcentral/fileexchange/3540
Hope this helps.
@Krishna
In the Frequency domain, each sub carrier will still see a complex gaussian random variable, but they wont be independent..
for OFDM since we take the Fourier transform of the channel, , in the freq domain, the random variables will have a covariance matrix of FAF^H
where F is the Fourier transform matrix and A is the diagonal matrix that contains the powers of the taps in the time doamin
and F^H denotes the Hermitian of the matrix
@Arun: Were you suggesting that the channel response in frequency domain will be correlated?
For the time domain channel, I have assumed 10 tap Rayleigh channel with each tap having an idependent random variable. In that case, what will be the covariance matrix A for that channel? Kindly clarify.
Hello Krishna, thanks for ur nice work on OFDM.
I have run ur simulation of ofdm in rayleigh multipath channel with and without cyclic prefix. But I dont get any difference in the result.why? where actually this thing work?
How can I use the doppler shift in the rayleigh simulation?
is there any problem if we use the Matlab build-in function chan = rayleighchan(ts,fd) as channel estimation?
@Masum: My replies:
1. Its surprising that you were able to obtain similiar performance with and without cyclic prefix in a multipath channel. How many taps were your channel. And what was your cyclic prefix duration?
2. Sorry, I have not tried modeling doppler.
3. I have not used rayleighchan() function. Hence unable to comment.
hello sir..
i am working on designing a complete adaptive modulation system..can you guide me?
@pulkit: I have not worked much on adaptive modulation. What is the level of guidance which you are expecting?
Hi Krishna,
Is multipath channel = ISI channel?
@Allyson: In general, yes.
Note that for modulation types like OFDM, the multipath channel causes interference from the previous symbol to the cylic prefix of the current symbol (and since cyclic prefix is ignored, the channel can be treated as flat fading for individual subcarriers).
hi krishna
do you codes for the effect of change in cyclic prefix length on BER,POWER,etc…PLz help me
@Ravi: Well, you can play with the code provided in the post, try for different values of cyclic prefix etc.
Please, could you help me to derive the BER equation of OFDM with Walsh-Hadamrd spreading in Rayleigh fading channel.
@Ahmed: Well, if there is a corresponding de-spreading algorithm at receiver, then the BER performance should be similiar to what we have obtained here in this plot. Agree?
hullow..
krishna can u help me to understand more about the performance of BER in BPSK….
Why the performance of BER are degrades while the SNR are increased? there is another reason????
@nyna: You may refer to the post on BER for BPSK in AWGN
http://www.dsplog.com/2007/08/05/bit-error-probability-for-bpsk-modulation/
Hello Krishna:
I have a doubt, I hope you can help me, what happend if I need to use V-blast and the taps are uncorrelated and obey an exponential power delay profile, E{|hk|2} = Cexp(-a k) and it is assumed that the channel does not vary over two OFDM symbols. How can I simulate this in Matlab
@Rajuelo: Well, for the 802.11a systems, we typically characterise the performance using the Naftali channel model. You may find more details about it in the following link:
Modeling Multpath in 802.11 Systems
http://www.commsdesign.com/article/printableArticle.jhtml?articleID=16505977
Hope this helps.
hi Krishna,
thanks for your code.
but how can i add the transmission loss(path loss) to the channel and plot the BER after that.
thanks in advance
in this programme , i don’t understand some codes
please , prove these codes
% Taking FFT, the term (nFFT/sqrt(nDSC)) is for normalizing the power of transmit symbol to 1
xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xF.’)).’;
how, the power of transmitt sympol
normalize to 1
sum(abs(xt(1,:).^2)) do not equal to 1 ??????
sum(abs(xt(:,1).^2)) do not equal to 1 ???????
@najat: We are trying to make E{|x(t)|^2) = 1. So try mean(abs(xt(1,:).^2)). This should be equal to 1. Agree?
hi krishna:
please aswer me
After viewig your program with title “Script for computing the BER for BPSK in OFDM modulation in the
of Rayeligh fading channel” I have some quieries about the code in program .In this code “
Taking FFT, the term (nFFT/sqrt(nDSC)) is for normalizing the power of transmit symbol to 1
xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xF.’)).’;
converting to frequency domain
yF = (sqrt(nDSC)/nFFT)*fftshift(fft(yt.’)).’;
you said that you multiply with factor to make normalization 1 .please can you prove me that.
With best regard.
Dear Dr krishna:
Please reply me as soon as please.You do ot reply to my questio . Please it is an urgent case for my proposal to master degree please .
With best regards
@najat: Sorry for the delayed response. We had internet outage at our place. Good luck in your studies.
hello krishna,
could you please explain the significance of using .’ in the code
xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xF.’)).’;
why does it not work when i use
1) xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xF(:,1:52)));
or do seperately as
2) xt = fftshift(xF(1:52));
xt = (nFFT/sqrt(nDSC))*ifft(xt(1:52));
Thanks
@kishore: I recall xF is a vector of 64 elements. And the 52 modulated subcarriers are not the first 52. Leaving guard subcarriers and not using DC subcarrier, we use subcarriers [-26:-1 1:26]. Agree?
hi kirshina
on the above post you calculated BER with out the erfc functions can you explaine why it is written that way.i have seen the same formula in some books for it said if only for one tap.
thanks
@kebede: You may refert to the posts on Derivation of BER for BPSK in Rayleigh channel
http://www.dsplog.com/2009/01/22/derivation-ber-rayleigh-channel/
please, can you help me?
how i can explain the gain of diversity between ZF and MMSE by therory?
for exemple in my simulation of ZF and MMSE BER=f(RSB), for 0.001 error rate, i have RSB=2 db of gain .
but i dont understand this result virtually.
@med: Sorry, I have not tried to evalue the theoretical difference between the ZF and MMSE. What is RSB?
Dear,
can you explain why are you coverting from dB once with factor 10 and another one with factor 20 ?
I mean those lines:
EbN0Lin = 10.^(EbN0dB/10);
yt = sqrt(80/64)*xt + 10^(-EsN0dB(ii)/20)*nt;
Thank you !
@joel: The noise is a voltage term and hence scaled by 20.
The other one is converting power in dB to power in linear, hence used the factor 10.
Agree?
Of course, you are right.
Thank you !
Mr Krishna,
I want just to know if you have an idea on Performance of an OFDM Communication System under a Frequency and Time Dependent Channel, I will appreciate your comment on that.
@chris: Most of the OFDM systems are expected to work in channel which is varying in frequency. However, for each subcarrier the channel experienced will be of flat fading and will be equalized by a single tap equalizer.
If the channel is time varying, quite likely the system should have mechanisms to track the channel. This can be achieved by having periodic preambles and/or hard decision decoding based channel tracking.
Dear Krishna,
can u explain how do we have in general to scale the energy (power ?) of a time signal in order to get the mean power of 1 after ifft (or fft). What are the scaling factors that the ifft (or fft) introduce ?
Thank You !
Regards
@joel: My replies
1/ Well, we typically scale the transmit power to 1 such that we can have precise definition of SNR when we compute BER or when we compare different modulation schemes
2/ Scaling factor introduced by FFT/IFFT depends on the implementation. In Matlab, fft() has scaling of 1, whereas ifft() has a scaling of 1/N
Plz refer to the link for more details.
Mr Krishna
Thanks for ur support I want to know that how can i use
hF=fft(ht,64,2); command in place of
hF = fftshift(fft(ht,64,2)); if there is no alternative then pls explain me about these commands
hF = fftshift(fft(ht,64,2));
xt=(nFFT/sqrt(nDSC))*ifft(fftshift(xF.’)).’;
Mr Krishna
Thanks for ur support I want to know that how can i use this command
hF=fft(ht,64,2); in place of
hF = fftshift(fft(ht,64,2)); if there is no alternative then pls explain me about these commands
hF = fftshift(fft(ht,64,2));
xt=(nFFT/sqrt(nDSC))*ifft(fftshift(xF.’)).’;
hi Krishna,
I workinig on simulink model – BER for DQPSK with AWGN, Rayleigh and LMS equalizer, and I dont know how can I get BER wich congruent with teoretical BER.
Do you have any example for this?
@nany: Sorry, I have not tried modeling LMS equalizer.
hello krishna,I fully respect your work! now i have a question about OFDM,’Though the total channel is a frequency selective channel, the channel experienced by each subcarrier in an OFDM system is a flat fading channel with each subcarrier experiencing independent Rayleigh fading’you said,Now i have got the results of BER performance in SISO OFDM with 16Path of Rayleigh multipath channel. But the BER perforance of MMSE,ZF and MLD is same to flat Rayleigh case, can you give me the theory poof of it or give me some reference information?
@Risou: Even if we have 16path rayleigh multipath channel, if the cyclic prefix is of duration more than the channel, each subcarrier will be experiencing flat fading. If there is no Inter Symbol Interference, i think that the ZF is optimal. That might explain why you are getting identical curves for MMSE and MLD cases.
Hope this explanation helps?
Dear Krishna,
I would like to ask you about the current IEEE 802.11 a/g/n for wireless LAN.
From what I read, OFDM is used with several choice of modulation and coding.
How the modulation and coding are varied in the OFDM transmission.
Do they implement adaptive modulation and coding yet?
Thank you very much
@hanne: In typical PHY specifications, there will be multiple data rates which are created using a combination of modulation scheme and coding rate. For eg, in 802.11a we have 6Mbps (using BPSK) and 54Mbps (using 64-QAM). Plz check Table 78 in the 802.11a specification You may use the link to http://standards.ieee.org/getieee802/download/802.11a-1999.pdf to download.
Which data rate to use is decided by the higher layer (MAC) based on packet error rate statistics.
Dear Krishna,
Thank you for your reply.
I will refer to that document.
By the way, i just want to ask you whether the modulation and coding in OFDM is varied by subcarrier or by the whole carrier.
For example can different subcarrier use different modulation and coding in one transmission?
TQVM
@hanne: Well, theoretically each subcarrier in an OFDM system can have a different modulation scheme. Having a different coding scheme on each subcarrier might be difficult as it might require per subcarrier coding. In typical specifications like 802.11a/n all the subcarriers in a stream uses the same modulation scheme.
Thank you for your answer.
Now I understand the current practice.
Khrisna,
Thank you for your reply for my email. I admit that i used bit energy instead of symbol energy. I am fixing my program now. May i know the reference you used for this article, especially about relation between bit energy and symbol energy in OFDM?
@Filbert: Well, I did not use any article as a reference. I just played with the variables and selected the one which was mathematically valid:)
hello Mr. pillai i am currently pursuing my masters and working on secure communication using ofdm actually i am stuck up at a place…….were we have to estimate the mutual channel between two user….the channel model is assumed to be simple block fading model frequency band is split into D coherence bands, with Nc = N=D OFDM tones per coherence band.We are considering a MMSE channel estimator for which the channel estimate generally takes the form hi = hi + ¢hi.¢hi is the error in estimate….i will be highly obliged if u can guide me on this matter….
@tahir: You might be able to formulate it as a classical MMSE problem, where you try to find a set of cofficients W which minimizes the mean of the square of the error between observed (noisy) and ideal channel coefficients. Typically MMSE solution reduces to
W = R{xy} R{yy}^-1 where
R{yy} – is the auto-correlation of the noisy channel estimate
Rx{xy} – is the cross-correlation between noisy channel estimate and ideal channel estimate
Hi Krishna,
What’s the purpose of shifting the frequency sub carriers before performing the ifft?
xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xF.’)).’;
Cheers,
Minh
@Minh: In the code, I have defined the subcarriers in the range from [-N/2 to N/2-1]. However, the ifft() function expects inputs to be in the range from [0 to N-1]. So the subcarriers from [-N/2 to -1] were shifted to [N/2 to N-1]. The post http://www.dsplog.com/2007/06/17/interpreting-the-output-of-fft-operation-in-matlab/ discuss this in bit more detail.
Hi krishna,
can u plz tell me how to calculate the delay(in terms of time) between the two multipaths….and how to change the delay because i am studying the effect of changing delay between the two multipaths…
Thanks.
@Ali: Well, did you mean that you wish to find the delay between two taps where the multipath coefficients are defined digitally? If you know the sampling period used for defining multipath, that should be reasonably easy, agree?
sorry,I can’t understand how to calculate the delay between the two multipaths in the matlab code provided by you…can u guide me specificallly how to calculate the time delay btw the two multipaths(if the number of taps is set to 2)???
@Ali: Whats your sampling frequency?
Lets say, the sampling frequency is 1MHz, then if the taps are defined as
h = [ coeff1 0 0 coeff2]; then the time delay between the taps is 3us.
Makes sense?
I am doing it in digital….not converting frm digital to analog and then back frm analog to digital….nd also i m doing baseband…. i have used this code of your’s to simulate…if i use nTap=2 in your code,then can u tell me how to calculate the delay?
Hi krishna,
can u plz tell me how to calculate the delay(in terms of time) between the two multipaths….and how to change the delay because i am studying the effect of changing delay between the two multipaths…
Thanks.
im stuck with frequency selective fading aspect of my project
its not with OFDM, but with single carrier frequency domain equalization..
today i went to see my supervisor
to show her the codes i had and the results(which are a bit off target in terms of Eb/No)
supervisor gave me hell
asking me why i had not implemented frequency selective fading
now she wants me to do this
IMPLEMENT A CHANNEL THAT EXHIBITS FREQUENCY SELECTIVE FADING!!!
now consider the code below!
% ——————————————————————- %
% Parameters Declaration %
% ——————————————————————- %
% Initialize the parameters
FrameNum = input(’number of frames transmitted is(default=5000) =’);
if isempty(FrameNum)
FrameNum = 5;
end
FrameSize = input(’size of each frame is(default=256) =’);
if isempty(FrameSize)
FrameSize = 256;
end
Chan =input(’channel IR is(default=[0.227 0.46 0.688 0.46 0.227]) =’);
if isempty(Chan)
Chan = [0.227 0.46 0.688 0.46 0.227]; !!!!!!!!!!!!!!===============
end
CPLen = FrameSize/8;
% ——————————————————————- %
% Generate Transmit Signal & BPSK Modulation %
% ——————————————————————- %
% generate the random binary stream for transmitting
BitsTranstmp = randint(1,FrameNum*FrameSize);
% modulate ,generate the BPSK symbols
Table=[-1 1];
% After the step upon,Table = [-1.0000-0.0000i 1.000]
BitsTrans = Table(BitsTranstmp+1);
% ——————————————————————- %
% Add CP %
% ——————————————————————- %
% the function RESHAPE is to rearrange the BitsTrans to add cp for con-
% venience
AddCPtmp = reshape(BitsTrans,FrameSize,FrameNum);
AddCP = zeros(FrameSize+CPLen,FrameNum);
AddPrefix = FrameSize-CPLen+1:FrameSize;
% the matrix below is as the same function of add cp to each frame one
% by one
AddCP = [AddCPtmp(AddPrefix,:);AddCPtmp];
% ——————————————————————- %
% Go Through The Channel %
% ——————————————————————- %
RecChantmp =filter(Chan,1,AddCP);!!!!!!!!!!!!!!!!!==============
notice the two lines with the marks of exclamation followed by ========= sign
first one
there is some declaration of CIR parameters which are applied to our bits to be sent in the second HILIGHTED command
now
what exactly is the function of doing this??
and how this affects our data??
at present, just help me with the frequency selective part!
howto implement a channel that exhibits frequency fading……..
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP!!!!!!!!!!!!!!????????????
hi:sir
I try to write the matlab code about multiuser detection for STBC
coded OFDM system,but it is not easy.,for example ZF MMSE etc.
can you give me some advice about it. thanks!
@Wyl: The multi-user detection problem can be considered to be equivalent to decoding of a V-BLAST transmission. In the multi-user case, transmission from another user is the interference; in the V-BLAST case, transmission from other spatial dimension is the interference. There are some posts on equalizers in V-BLAST
a) MIMO with Zero Forcing equalizer
http://www.dsplog.com/2008/10/24/mimo-zero-forcing/
b) MIMO with MMSE equalizer
http://www.dsplog.com/2008/11/02/mimo-mmse-equalizer/
c) Six equalizers for V-BLAST
http://www.dsplog.com/2009/04/21/six-equalizers-for-v-blast/
Hope this helps.
sir
plz help me out for matlab programs of MCCDMA (transmitter & receiver)
racien fading any programs of matlab regarding MCCDMA
thank u,
pragya
@pragya: Though I have not discussed MC-CDMA explicitly, I would guess that problems in equalization can be treated similar to OFDM case and the Matlab code in this post gives an example for equalization in Rayleigh multipath channel model. Agree?
Krishna, while studying your simulation code I noticed that you are adding a cyclic prefix before the P-2-S converter at the transmitter. Shouldn’t it be after the P-2-S converter?
Waiting for your reply
@Communications Engineer: The cyclic prefix is added in the time domain. It happens after the serial-to-parallel conversion (which happens at the ifft) in the transmitter.
sir:
Thank you for your advice!I want to know how to write the matlab code
about the multi-user MIMO-OFDM Rayleigh channel,I have modified your code ,I don’t know it is right? My code:
k=2; %user numbers
Nc=128;%subcarrier number
cp=32;
sym_per_carrier=6;
signal=rand(k,Nc*signum_per_carrier);
%through Rayleigh channel
H=sqrt(1/2)*(randn(nr,nt,addcp*signum_per_carrier,k)+i*randn(nr,nt,addcp*signum_per_carrier,k));
In order to give you less trouble, I have cut the part of the code. for every user,use for language to change the 1th and 2th row to Nc row,ifft and add cp ,then through the Rayleigh channel and add noise.
At receiver,I use ZF Algorithm to detect each user.
my code:
for i=addcp*signum_per_carrier
for user=1:k
G=pinv(H(:,:,i,user))
r=G*y
end
end
I don’t know my thout is right? can you give me some advice? thank you very much!
@Wyl: Sorry, I still could not understand. Some questions:
1/ Does each transmitting user has a multiple transmit antennas?
2/ How many antennas at the receiver?
Hi Krishna,
Regarding the taps coefficients; if I wnat to make them spaced by 2 or 3 samples for example; how can we modify your code?! can I simply upsampling the channel taps vector (adding zeros)?
Thanks,
@Khalid: Yes, add zeros inbetween channel taps.
Thanks krishna:)
Hi krishna
BER for Rayleigh fading channel with or without using OFDM is same. Plz can u comment on this?
@Neetu: Infact, BER for flat fading Rayleigh channel is same as BER for frequency selective Rayleigh channel with OFDM. This is because, thanks to OFDM, even though the channel is frequency selective, the channel experienced by each subcarrier is still flat fading. Also note that, since channel duration is lower than the cyclic prefix, there is no inter symbol interference. Hence the performance is the same.
Sir,
I want to know about the relation between SNR & PAPR?
@SUBHA: Hmm… no relation. PAPR is the measure of peak signal power by average signal power.
SNR is the measure of average signal power by average noise power.
HELLO SIR,
THANK YOU FOR REPLY.
Sir, How to caculate SNR of WiMAX?
@SUBHA: From the receiver bandwidth, we know the noise floor. Then we might also know the received signal power. Using both the above information, we can find the signal to noise ratio.
and, if the distance btw two consecutive tap is 50 ns, then the taps should be equidistant….kindly explain.
@ali: Need not be. We can have situations where some of the tap values are zero. In that case, the distance between tap values are not the same always.
HI Krishna
I have read the proof that you have given for BPSK in flat rayleigh fading. It is brilliant presentation.
What I would like to know is that how can I derive an upper bound for frequency selective maultipath channel (Time invariant case, lets say Proakis Channel B) for MMSE linear equalizer. I am getting the BER plot that he has given in the book but I am interested in the upper bound.
It will be really great if you can suggest some papers or anything that can be useful.
Thanks
Chintan Shah
@Chintan: You have to thank Mr. Jose Antonio Urigüen for providing the proof. Sorry, I do not have references for the topic which you have suggested.
plz tell me is that 1o-tap rayleigh channel is a frequency selective chnnel, which is later converted to flat fading channel..ie each subcarrier will suffer flat fading
tel me am i right or wrong?
quick response is appreciable
thanks very much
keep up the gud work
@mak_m: You are right. For each subcarrier, the channel is flat fading.
plz tell me is that 1o-tap rayleigh channel is a frequency selective chnnel, which is later converted to flat fading channel..ie each subcarrier will suffer flat fading
tel me am i right or wrong?
quick response is appreciable
thanks very much
keep up the gud work
I am working over for the thesis work in channel estimation.pl can i be helped for matlab codes for the same??
@manoj sharma: Channel estimation in typical wireless communication happens by using known preamble sequence. For eg,
y = hx + n, where
y – is the received symbol
h – is the channel
x – is the known preamble,
n – is the noise
Simplest estimate of channel is
h estimate = y/x
Good luck.
hi
i knew that OFDM technique improve BER performance in frequency selective fading channel
you can help me in
writing program for BER for binary phase keying modulation in frequency selective fading
and comparison with BER for OFDM technique also using BPK
@najat: I have not written post on BPSK single carrier in a multipath channel. Will do so in future.
Dear Kreshna
Can you help me in writing program for BER of psk modulation in frequency selective fading channel .My problem in how modeling the frequency selective and I want the references for the equations of your program.
Thank you
@Ahmad: I have discussed only frequency selective channel in OFDM case.
Dear Kreshna:
please reply me please .
Can you help me in writing program for BER of psk modulation in frequency selective fading channel .My problem in how modeling the frequency selective and I want the references for the equations of your program.
Thank you
Hi Krishna,
just wondering what ia the number 80 stands for?
64 is the nFFT size but 80 ???
EsN0dB = EbN0dB + 10*log10(nDSC/nFFT) + 10*log10(64/80);
@Marwan: For constructing the OFDM symbol, we have a 64 samples of data plus 16 samples of cyclic prefix, resulting in a 80 samples in an OFDM symbol. Cyclic prefix does not carry any extra information, rather just serves as a buffer zone for avoiding inter symbol interference (ISI) in multipath channel. Makes sense?
hi krishna,
i would like to know the difference between BER and PER.
and can you guide me in my project work.
title”Efficient spatial covariance estimation for Asynchronous co channel interference in MIMO OFDM systems”
pls i will looking forward for ur help
thanking you,
Sk Khaja rasool
pls : reply to this mail ID khajarasool_17@yahoo.com
@khajarasool:
BER – bit error rate
PER – packet error rate.
A packet will consist of multiple bits and even if one bit in the packet is in error, the packet is flagged to be in error.
nice site
hello Mr. Krishna,
i am a wireless communications master student, and i’m working on the simulation of the SDMA-OFDM system for 2 by 2 and 4 by 4 channels. I tried to combine your separate codes of OFDM, MIMO to build my system but i didn’t get anything correct, and i got a very lengthy and difficult code. Actually, i need your help regarding this, and i have some questions regarding your OFDM code.
1. why didn’t you use the same number of subcarriers as the size of the fft.
2. why did you use the subcarrier index for the subchannels?
i tried using the same as this code for 2 by 2 channel and i defined four random channel matrices to represent the four paths between the two transmit antennas and the two receive antennas. and then i applied the MMSE equation at the receiver after the fft operation, i used this equation on a per tone basis, and then at the end i compared the estimated and the actual bit streams, but, unfortunately, i got a straight line as a BER plot vs. the SNR. So, i would appreciate if you help me or give me some hints in this regard…Thanks
@samalqudah
1/ The subcarriers at edge are not used to avoid interference with other channels. The DC subcarrier is not used as zero IF receivers will have DC in the RF
2/ Subcarrier index is just a way of identifying the used subcarriers
Hello Mr. Krishna,
if i have the channel taps as a complex row vector in the z-transform representation, how can i get the channel impulse response in time, and how then to apply the frequency response of the CIR? if i want to use the invfreq command [a b]=invfreqz(h,w,n,m), so how can i know the w vector in the command(i don’t have any knowledge of w, from where should i get it?i just have h), and if the h i have is a complex row vector of order z^(-11) then n=11? and m=0?
Thank you
@samalqudah: Well, the channel can be modeled as an FIR filter. Lets assume that the
H(z) = 1 + 2z^-1 + 0.1z^-2
Then h[n] = [1 2 0.1]
H(f) = fft(h[n])
Agree?
Thank you for your post. I have read it and also all the comments. I have a question about multipath fading. In your simulation, all of the paths have the same gain, and you use the normalization that makes the same result with flat-fading channel. Therefore, if the paths that have different gains will result in worse quality, is it right and is it true in reality? Thank you
@minh: Well, I do not agree with the first part of your comment.
The fact that all paths have the same gain and the normalization does not make the channel as flat fading. Its the cyclic prefix in OFDM transmissions which make the channel equivalent to a flat fading channel.
In reality, each path may have an exponential distribution (for eg, see Naftali channel model)
http://www.commsdesign.com/article/printableArticle.jhtml?articleID=16505977
Thanks alot to u for providing such core details regarding ofdm n frequency selective channel . i hav got very gud marks in my masters project only bcoz of dsplog
keep continuing gud work.ur work is very helpful around the world
God bless u
@mak_m : Glad to hear. Thanks
Thank you for your post. I have read it and also all the comments. I have a question about multipath fading. In your simulation, all of the paths have the same gain, and you use the normalization that makes the same result with flat-fading channel. Therefore, if the paths that have different gains will result in worse quality, is it right and is it true in reality? Thank you
@minh: I normalize the channel taps such that the channel gain is unity. Such a channel in single carrier case would have given poorer performance compared to OFDM case. Thanks to cyclic prefix in OFDM, the multipath channel performance is comparable to flat fading.
Thank you for your reply. However, I still want to ask you about the result in reality, when paths have different gains and the normalization will make the path gains worse. Thank you.
@minh: Well even if the paths have different gain, but if you still make the total channel gain to unity, I expect you should get similar performance. Did you try? Can you please share your results.
Dear Krishna,
Thanks for your excellent works. However, I am littlle bit confused how the term (nFFT/sqrt(nDSC)) is normalizing the power of transmit symbol to 1. Would you please help me in this regards?
Thanking you
Anwar
@Anwar: The term 1/sqrt(nDSC) is used because we are using only nDSC subcarriers. The term nFFT is used to remove the effect of normalization by 1/nFFT, which is present in ifft() function.
of course i agree, thank you mr. krishna
Hi Krishna:
Your blog is very good.
Can you explain equation for Es/No in details? Also I am confused about
sqrt(80/64) term used in code to account for wasted energy of CP. Would you please delve more into it?
yt = sqrt(80/64)*xt + 10^(-EsN0dB(ii)/20)*nt;
Are we multiplying ‘nt’ with its sqrt(variance) corresponding to Symbol to NR? I mean, is 10^(-EsN0dB(ii)/20) = sqrt(sigma_n^2) here? Please, explain. I am getting confused with scaling factors.
Thanks.
@Toufiq: My replies
1) The 16 samples out of 80 received samples are ignored by the receiver. This means that the noise added onto those samples does not corrupt the demodulation. To make the simulation model accurate, so we scale the transmit power by sqrt(80/64)
2) Yes. The noise term nt is multiplied by square root of variance.
I am waleed from Palestianian
I was in need the lms beamforming for pre and post-fft processing ofdma communiation system.
thank you for all
@waleed salos: Sorry, I have not discussed LMS beamforming.
Hallo,
your code had helped me a lot. Thank you very much.
I have a question to your code. The frequency response of the channel
in your code didn’t use the FFT scaling factor. why ?
i think , it schould be : HF=fftshift(fft(ht,64,2))/sqrt(nFFT)
i have tried with this scaling factor, but then the result became wrong
Can you explain me that? Thank you very much
@xero: I think since am using BPSK, any normalization error at the receiver should not really matter. Were you using BPSK?
When you said – “results became wrong”, was it 100% errors?
Krishna,
Thanks for uploading such good codes and continuous updates. They are extremely helpful.
I have couple of queries regarding OFDM in rayleigh fading cahnnel.
1)Is there any difference between no. of paths and no. of taps for multipath channels?
2)You have mentioned about using a FFT sampling frequency of 20Mhz.
Would you please explain how this value is used in the simulation since (if I am not mistaken) I couldn’t find any reference to this value in the code.
3)In one of your replies you mentioned about applying zero-forcing equalization.
The code line
yF=yF/.hF
is its implementation. Is it a correct understanding?
4) As per my understanding , in OFDM the receiver as well as the (transmitter) is assumed to work in frequency domain, thus if we consider applying receiver diversity for OFDM system, can you suggest the fundamentals modifications that are needed (if any) in your codes regarding receiver diversity (mrc, ecg, selection) which I feel is written in the essence of time domain.
Thanks in advance
Regards
Ahmed
@Ahmed: My replies
1) No, they mean the same
2) The concept of sampling frequency is notional in Matlab. For eg, in a vector x = [1 2 3 4 5], the duration between 1 and 2 can be 1s or 1 us or any other number. In our simulation the gap between each sample at the output of the ifft is assumed to be 50ns (and hence the fft sampling frequency is 20MHz).
3) Yes
4) You need to have one more receive chain (i.e one more fft). The receive chain gets information from an independent channel. The output of the fft from multiple receive chains can be processed in any of the diversity combining ways.
Good luck in your explorations
hi krishna
ur script is really appreciable. actually i am workeing on a problem when the number of taps are greater than cyclic prefix. in your code i made nTap=20 becoz cp=16 and rest everything same. then i run your codes. by doing this it gives wrong results. what should i do plz help
@Bhasker: Well, can you please tell bit more why you consider the results to be wrong? What is your expected result?
Actually i want to analyze BER performance under frequency selective fading.
so for this i increased tap length from 10 to 20 i.e higher than CP. i run your code just after changing nTap from 10 to 20. it showing some error. plz help
can you plz tell me what sort of equalization i shoud employ for the above scnerio.
Hello Krishna,
no, i am not using BPSK, but the 64QAM. Sorry, i forgot to tell you this…
if i change the HF from fftshif(fft(ht,64,2)) to fftshif(fft(ht,64,2))/sqrt(64), then the symbol error rate becomes 1(100%). Without this scaling factor , the SER curve matches the theoretical curve of 64 QAM SER under Rayleigh channel, which is(M=64):
alpha =4;
beta = 3/(M-1);
theorySer= alpha/2*(1-sqrt(0.5*beta*(10.^(EsN0dB/10))./(1+0.5*beta*(10.^(EsN0dB/10)))));
thank you very much.
@xero: Well, if you add the scaling factor in the transmitter, make sure that you inverse the effect of scaling when performing demapping of the bits from constellation points. For 64-QAM, we set our constellation thresholds assuming constellation at {+/-7,+/-5,+/-3, +/-1}. If you have the scaling by 1/sqrt(64), you can either multiply by sqrt(64) in the rx or adjust the thresholds for making the decision
hi, how are you?
is there any way to convert this BPSK mod to QPSK mod?
Will it have the same result with this?
@Matlab’s: Please have a look @
http://www.dsplog.com/2007/11/06/symbol-error-rate-for-4-qam/
* genearte large no of bits using randint
* modulate the data once with bpsk & then 16-QAM
* bpsk mod is 2*data-1
* after modulation u should loop on the data with step of 64’s
each time calculating their ifft
* add the noise to each 64
* if u remeber how to add noise then do it as u know,
else use awgn
sigandnoise=awgn(signal, SNR in dB , ‘measured’ )
* do fft with steps of 64’s , the same groups of symbols that were ifft’ed
* demodulate the data ( if bpsk then bits= recdata > 0)
*calculate ber using
ber=sum(xor( transmitted bits , received bits ) )
* the whole program should be done in a large loop that loops over
SNR -5 -> 15
* in case of fading
multiply with channel before ifft then divide after ifft
* multiplication is done using (.*) not just (*)
Hi Khrisna,
If i use QPSK, what should i use for x-axis, Eb/N0 or Es/N0?
Thank you
Hi Krishna,
I tried to change tap number ,but I couldn’t see a difference in BER.Isn’t it suppossed to be change?
Thanks from now.
sir plz answer my previous query.
i got bit confused in frequency selective channels. should i always need channel estimation before equalization in frequency selective channels in OFDM systems.
sir i am getting no answer regarding previous queries. i am requesing u to reply them asap
sir i have one more doubt. actually i want to compare ofdm performance with and without equalizer in frequency selective channels.
in above script i changed nTap to 20 for getting frequency selective channel. then i run the code with and without equalizer.
with equalizer it seems ok but without equalizer it showing straight line BER curve plz help.
Hi Krishna,
I was looking at your BER curves for BPSK in OFDM with and without Rayleigh multipath fading channel.BER curves shown by you in both cases are similar but isn’t OFDM suppose to provide resilience to degradation in the signal strength due to multipaths and frequency selective fading? Please clarify the advantages of using OFDM in multipath fading scenarios…
Thanks
Ishwinder
Hi Krishna,
If i do k/n rate Convolution encoding, how does it change the theoretical BER equation for BPSK, QPSK, 16QAM and 64 QAM? Do you have some visibility on this?…
Thanks
Ishwinder
Hello Krishna,I have a problem in simulating OFDM rayleigh fading multipath using 16QAM.More precisely,I am simulating a flat fading channel
along with the 4 ITU-R channel Models Pedestrian A and B,Vehicular A and
B.I am expecting the ber curves for the 5 models to coincide since I am using
Cyclic Prefix duration longer than the largest delay spread.Isn’t that so??Instead I get only the pedestrian A and flat fading curves almost the same,whereas the others not.Have you any idea what could be wrong in these case??Here is my code:
close all
clear all
clc
M = 16; % range of data symbols
k = log2(M); % number of bits per data symbol
N_OFDM_Symbols = 10;
N_FFT = 128; % number of subcarriers used in an OFDM symbol
EbNo = 0:1:20;
CP = 40; % number of subcarriers used for the Cyclic Prefix
Tsymbol = 1/10e6;
W = 10e6; % bandwidth
Df = W/N_FFT; % distance in the frequency domain between subcarriers
fc =2.5*10^9 ; % main frequency
data_modulator=modem.qammod(M); % M-QAM modulator
data_demodulator=modem.qamdemod(M); % M-QAM demodulator
f=(fc-W/2)+((1:N_FFT)-1/2)*Df ; % value of frequency for each of the N_FFT subcarriers
H=zeros(1,N_FFT);
channelModelName = { ‘Flat’, ‘PedA’, ‘PedB’, ‘VehA’, ‘VehB’ } ;
NumOfErrors=zeros(length(channelModelName),length(EbNo)); % Array of Errors in transmitted symbols for each value of EbNo
channelModel_cnt=0;
for channelModelNames=channelModelName
channelModel_cnt=channelModel_cnt + 1;
channelModel = defineChannelModel(channelModelNames{1});
a = channelModel.PathPower_dB ; % vector with path channel gains in dB
t = channelModel.PathDelays_usec*1e-6 ; % vector with path delays
L = length(t);
%Calculation of Channel Impulse Response
for l=1:L
H =H +(randn+1i*randn).*(10^(a(l)/10))*exp(-1i*2*pi*f*t(l)); % channel impulse response
end;
H_Chan=H’;
for ebno_cnt=1:length(EbNo)
ebno=EbNo(ebno_cnt);
snr=ebno+10*log10(k) + 10*log10(N_FFT/(N_FFT+CP));
for N_OFDM_Symbols_cnt=1:N_OFDM_Symbols
% Transmitter
% Frequency Domain
data_symbols=randi([0 M-1], [N_FFT, 1]); % unmodulated symbols
mod_data_symbols=modulate(data_modulator,data_symbols); % modulated symbols
% Time Domain
; mod_data_samples]; % Addition of cyclic prefix
mod_data_samples = sqrt(N_FFT)*ifft(mod_data_symbols,N_FFT); % Inverse Fast Fourier Transform
mod_data_samples_w_CP=[mod_data_samples(N_FFT-CP+1:N_FFT,
% Frequency Domain transition through FFT
; H_Chan ];
% Data through Rayleigh channel
mod_data_symbols_w_CP=1/sqrt(N_FFT+CP)*fft(mod_data_samples_w_CP,N_FFT+CP);
H_chan=[H_Chan(N_FFT-CP+1:N_FFT,
mod_data_symbols_w_CP_chan =H_chan.*mod_data_symbols_w_CP ;
% IFFT
mod_data_samples_w_CP_chan=sqrt(N_FFT+CP)*ifft(mod_data_symbols_w_CP_chan,N_FFT+CP) ;
% AWGN channel
received_mod_data_samples_w_CP=awgn(mod_data_samples_w_CP_chan,snr,’measured’); % addition of awgn
% Receiver
received_mod_data_samples=received_mod_data_samples_w_CP(CP+1:N_FFT+CP,:); % Removal of Cyclic Prefix
%Fast Fourier Transform – Frequency Domain
received_mod_data_symbols=1/sqrt(N_FFT)*fft(received_mod_data_samples,N_FFT);
% Channel compensation
received_mod_data_symbols= (conj(H_Chan)./(conj(H_Chan).*H_Chan)).*received_mod_data_symbols;
received_data_symbols=demodulate(data_demodulator, received_mod_data_symbols); % demodulated symbols
% Calculation of error symbols
[tNumOfErrors,~] = biterr(data_symbols, received_data_symbols);
NumOfErrors(channelModel_cnt,ebno_cnt) = NumOfErrors(channelModel_cnt,ebno_cnt)+tNumOfErrors;
end;
end;
end;
semilogy(EbNo,NumOfErrors/(N_OFDM_Symbols*N_FFT));
hold on;
xlabel(’EbNo’);
ylabel(’ber’);
title(’plot of BER vs EbNo’);
legend(channelModelName);
I am also using the following function defineChannelModel in another m-file:
function RValue=defineChannelModel(ChannelModelName)
Flat = struct(’Name’,'Flat’,'PathPower_dB’,0, ‘PathDelays_usec’,0 );
PedA = struct(’Name’,'PedA’,'PathPower_dB’,[0 -9.7 -19.2 -22.8], ‘PathDelays_usec’,[0 110 190 410]*1e-3 );
VehA = struct(’Name’,'VehA’,'PathPower_dB’,[0 -1 -9 -10 -15 -20], ‘PathDelays_usec’,[0 300 700 1100 1700 2500]*1e-3 );
PedB = struct(’Name’,'PedB’,'PathPower_dB’,[0 -0.9 -4.9 -8 -7.8 -23.9], ‘PathDelays_usec’,[0 200 800 1200 2300 3700]*1e-3 );
VehB = struct(’Name’,'VehB’,'PathPower_dB’,[-2.5 0 -12.8 -10.0 -25.2 -16.0], ‘PathDelays_usec’,[0 300 8900 12900 17100 20000]*1e-3);
switch ChannelModelName
case ‘Flat’,
RValue = Flat;
case ‘PedA’,
RValue = PedA;
case ‘VehA’,
RValue = VehA;
case ‘PedB’,
RValue = PedB;
case ‘VehB’,
RValue = VehB;
otherwise,
throw(MException(’VerifyOutput:OutOfBounds’, ‘Unknown Channel Model’));
end;
Dear Krishna
What would be the performance of above code it the channel taps are not independent Gaussian random variables with mean 0 and variance 1/2.
I am asking because I am doing a simulation on a 10-taps channel. The taps’ amplitudes are generated through a procedure and taps’ phases are chosen to be uniformly distributed. Cyclic Prefix is 16 which is greater than number of channel taps (10). Following lines of code have been used to generate the complex taps and convolution.
ht1c=ht1.*exp(j*2*pi*rand(size(ht1))); %complex taps ht [10-by- 1]
ht1c = ht1c./max(abs(ht1c)); %normalizing channel taps’ magnitude to 1
xh=conv(ht1c,x); %convolving with the input with channel
But this gives me a curve approx. 5 dB better than the theoretical Rayleigh flat fading curve.
Any clue! Why is it happening? Your help is really appreciated
Regards
Anser
@Mehboob: Can you please tell how you are generating ht1
is it by ht1 = 1/sqrt(2)*1/sqrt(nTap)*(rand(nSym,nTap) + j*rand(nSym,nTap))
Quite likely, the variance of the ht1 is reason for seeing better performance.
Hi Krishna
Thank for your response. Actually, the amplitude of my ht1 isn’t following Rayleigh distribution – its just decaying exponentially with a miximum and minimum values pre fixed using following lines of code.
Th=1e-6; %Th=Impulse response delay
Np=10; % Np= Number of Paths
i=0:Np-1; % ith path from 0 to Np-1
ti=(Th/(Np-1))*i;
b0=0.01;
b1=0.002;
ht1=(b0*(b1/b0).^(ti/Th)); %this generates an exponential decaying
%function with maximum amplitude=
%bo=0.01 and minimum amplitude=
%b1=0.002;
And in the following code I am just multiplying taps’ amplitudes (ht1) with a random phases terms. I dont think here I would need to normalize the exp(j*2*pi*rand(size(ht1))); term with 1/sqrt(2)*1/sqrt(nTap) because amplitude of exp(j*2*pi*rand(size(ht1))) is already 1 – I am only interested in its phase which can only be affected by (j*2*pi*rand(size(ht1))) term.
Thanks
Anser
ht1c=ht1.*exp(j*2*pi*rand(size(ht1))); %complex taps ht [10-by- 1]
ht1c = ht1c./max(abs(ht1c)); %normalizing channel taps’
%magnitude to 1
xh=conv(ht1c,x); %convolving with the input with channel
thanks for your your graet work
please I study for my master in frequency synchronization in mimo ofdm system but i have problem with the matlab code to simulate to find out if estimation of the CFO on one path is affected by the CFO values of the adjacent paths and examine the estimator accuracy in term of its mean and variance
please help me it’s urgent and necessary
f_max = f_Tofdm/(M_sub*T_s); % f_max =maximal Doppler frequency (Hz),M_sub*T_s = OFDM Symbol period (sec),
%f_ndopp = f_max*M_sub*T_s % Normalized Maximum Doppler Spread Freq.
% Area parameter
% ra Rural Area
% tu Typical Urban
% bu Bad Urban
% ht Hilly Terrain
% no no fading
AREA = ‘no’ ;
% start simulation loops
for ee = 1 : length(EcNo)
ee
[theo_fo_var, rfo_var, rfo] = FOE_mimo_fading(EcNo(ee), tfo_array, NTX, NRX, M_sub, N, f_max, AREA, T_s, model, L);
plot_theo_fo_var(:,:,ee)=theo_fo_var;
plot_rfo_var(:,:,ee)=rfo_var;
plot_theo_rfo(:,:,ee)=tfo_array;
plot_rfo(:,:,ee)=rfo;
end
% plot results
for ii_tx = 1 : NTX
for ii_rx = 1 : NRX
% rearrange array order for easier plotting
vect_plot_theo_rfo = permute(plot_theo_rfo(ii_tx,ii_rx, , [2 3 1]);
vect_plot_rfo= permute(plot_rfo(ii_tx,ii_rx, , [2 3 1] ) ;
vect_plot_theo_fo_var= permute(plot_theo_fo_var(ii_tx,ii_rx,:),[2 3 1]);
vect_plot_rfo_var= permute(plot_rfo_var(ii_tx,ii_rx, , [2 3 1]);
%plot mean
figure;
plot(EcNo, vect_plot_theo_rfo, ‘:’ , ‘Linewidth’,2) ;
hold;
plot(EcNo, vect_plot_rfo,’o-’,’MarkerSize’ , 6,’Linewidth’, 1) ;
grid on;
t_str=sprintf(’New_ Theo and Est Freq Offset %s M=%d N=%d %dx%d path:tx%d-rx%d fo=%1.3f’,AREA,M_sub,N,NTX,NRX,ii_tx,ii_rx,tfo_array(ii_tx,ii_rx));
title(t_str);
xlabel(’EcNo SNR range and step (in dB)’);
ylabel(’Norm Freq Offset’) ;
legend(’Theo’,’Est’,’Location’,’Northeast’);
% save graph
fstr=sprintf(’new_m%d_%dx%dp%d%d_%s’,M_sub,NTX,NRX,ii_tx,ii_rx,AREA);
hgsave(fstr);
% plot variance
figure;
semilogy(EcNo, vect_plot_theo_fo_var,’:’,’Linewidth’,2);
hold;
semilogy(EcNo, vect_plot_rfo_var,’o-’,’MarkerSize’,6,’Linewidth’,1);
grid on;
grid minor;
t_str=sprintf(’New_ Est Var and CRLB %s M=%d N=%d %dx%d path:tx%d-rx%d fo=%1.3f’,AREA,M_sub,N,NTX,NRX,ii_tx,ii_rx,tfo_array(ii_tx,ii_rx));
title(t_str);
xlabel(’EcNo (in dB)’);
ylabel(’Variance’);
legend(’CRLB’,’Est’,’Location’,’Northeast’);
% save graph
fstr=sprintf(’new_y%d_%dx%dp%d%d_%s’,M_sub,NTX,NRX,ii_tx,ii_rx, AREA) ;
hgsave(fstr);
end
end
% rename variables for export
new_plot_theo_fo_var=plot_theo_fo_var;
new_plot_rfo_var=plot_rfo_var ;
new_plot_theo_rfo=plot_theo_rfo;
new_plot_rfo=plot_rfo;
% save all variables
fstr=sprintf(’new_f%d_%dx%d_%s.mat’,M_sub,NTX,NRX,AREA);
save(fstr);
% save variables for plotting
fstr=sprintf(’new_p%d_%dx%d_%s.mat’,M_sub,NTX,NRX,AREA);
save(fstr,’new_plot_theo_fo_var’,’new_plot_rfo_var’,’new_plot_theo_rfo’,’new_plot_theo_rfo’);
% end of file
@eng_dina: How are you modeling the CFO for MIMO systems?
If all the chains have a common RF clock, then all the chains will have similar CFO and the estimate from all the chains can be combined to improve the accuracy of the CFO estimation.
If the chains have independent RF clock, then we need to estimate CFO on each chain independently.
Idon’t try to simulte cfo for mimo system only but for mimo ofdm I propose a new scheme that targets MMIO OFDM systems which have unsynchronized oscillators such that CFO of individual paths have to be estimated separately. This scheme may also apply to OFDM systems with multi-user access. The new method, which is similar to Moose’s method, estimates the CFO by measuring the carrier phase difference between 2 identical successive training sequences embedded in the preambles. In order to make CFO estimates be more time efficient,I allow 2 transmitter antennas transmit their training sequence concurrently in every time period, except the first and the last period. I use Frank-Zadoff code with different phase shifts in the training sequences in different antennas. Due to the good correlation property of Frank-Zadoff code, it helps reduce the interference caused by the concurrent transmissions from other antennas.
please helpppppppppppppppppppppppp
sir,
how i will generate allocation of adaptive subcarrier for users in ofdma in matlab.
Idon’t try to simulte cfo for mimo system only but for mimo ofdm I propose a new scheme that targets MMIO OFDM systems which have unsynchronized oscillators such that CFO of individual paths have to be estimated separately. This scheme may also apply to OFDM systems with multi-user access. The new method, which is similar to Moose’s method, estimates the CFO by measuring the carrier phase difference between 2 identical successive training sequences embedded in the preambles. In order to make CFO estimates be more time efficient,I allow 2 transmitter antennas transmit their training sequence concurrently in every time period, except the first and the last period. I use Frank-Zadoff code with different phase shifts in the training sequences in different antennas. Due to the good correlation property of Frank-Zadoff code, it helps reduce the interference caused by the concurrent transmissions from other antennas.
please helpppppppppppppppppppppppp
please reply me it’s urgent Ineed the code it’s really important and thanks alot
Hallo,
your code had helped me a lot. Thank you very much.
Please can you help me if the channel became Nakagami-m multipath fading channel.
I do not know how to simulate Nakagami-m channel, please help me
im new in matlab.
Hello Krishna, thanks for ur nice work on OFDM.
i want to design an OFDM simulator using matlab GUI so that we can easily to find out the BER vs SNR when i change any parameter on the modulation..
can u give me some idea which part i need to change mybe on the sampling freq or mybe on the no of sample..
and lastly from ur code which part i must to do so…please teach me…-shah-
hello mr. krishna,
i would ask you a question regarding the rayleigh channel. how can i generate Rayleigh channel impulse response as ready numbers to be used in a program without using the rand()+j*randn() commands. in other words, i don’t want to have a loop or large number of symbols to get the plot of the prob. of error. I want to have a table of values for channel impulse response to be used for simulating a MIMO system. some papers do list down in a table the channel as complex values between each transmit and receive antenna to get a MIMO channel matrix, how did they get such values? this is exactly my question
Dear Mr.Krishna
plz i need to calculate BER in QPSK -OFDM With multi path rayleigh fading
can you help me
and if you want how can use PN sequence in QPSK
thanks alot
Hi Krishna,
I ran your script ” BER simulation of BPSK in OFDM with Rayleigh fading channel” . I observed that even when i set the number of taps(nTap parameter in the script) to 1, it results in the same curve.Should we not see a improvement in the BER as the channel is changed from a 10-tap multipath fading channel to 1-tap flat fading channel? Please provide your comments on this observation.
Thanks
Ishwinder
@communication: Yes, you are right that the continuous phase modulation schemes have a cleaner spectrum – relaxing the constraints on filter, PA’s etc.
I do not have Simulink available for me for the simulations for the blog. Yes, I am fine with having guest posts running on the blog. We recently had a blog on the derivation of BPSK BER in Rayleigh channel by Jose Antonio Urigüen
http://www.dsplog.com/2009/01/22/derivation-ber-rayleigh-channel/
Mr Krishna
Regarding your matlab code for OFDM using BPSK over Rayleigh Fading Channels. I tried but i failed to understand how u calculated these parameters.
nFFT = 64; % fft size
nDSC = 52; % number of data subcarriers
nBitPerSym = 52; % number of bits per OFDM symbol (same as the number of subcarriers for BPSK)
nSym = 10^4; % number of symbols
As according to my coding BPSK in OFDM. i have used 256 bits to transmit over 256 symbols i.e. 1 bit/symbol. Using 256 point fft and IFFT. So pls advice me how can i setup my parameters.
Acc to my knowledge in BPSK one bit is transmitted in one symbol and then it is furthur transmitted on the subcarrier.Pls correct me if i am wrong.
@raj: “Acc to my knowledge in BPSK one bit is transmitted in one symbol and then it is furthur transmitted on the subcarrier.Pls correct me if i am wrong.”
This is wrong. In OFDM, depending on the FFT size, there will be more than 1 subcarrier which is used. For eg, in 802.11a systems, we use 64pt FFT and use 52 subcarriers. If each subcarrier is BPSK modulated, then each symbol can carry 52 bits. Hope this helps.
Please refer to posts @ http://www.dsplog.com/tag/ofdm
@GRS: “cross-correlate the received signal with known channel” – we do not know the channel, do we?
@Ali: Whats your sampling frequency?
i have assumed the same 20 MHZ as u have…kindly give the procedure of calculating the delay….also,are all the multipaths equidistant from each other?
@Ali: If the sampling frequency is 20MHz, the delay between the two consecutive taps are 50ns. No, its not guaranteed that all multipath taps are equidistant from each other.
can u plz tell me how u calculated that.?
@ali: The inverse of sampling frequency i.e 1/20MHz = 50nano seconds
But should we at least sample at Nyquist’s criterion and select sampling frequency of 40 MHz to recover the 20 MHz bandwidth?
Or is this kind assumption is fine i.e. fs = 20 MHz
@communications engineer: For recovering an OFDM signal with bandwidth 20MHz, we need only a sampling of 20MHz. We use aliasing to our advantage here. For more details, please refer to the post on negative frequency
http://www.dsplog.com/2008/08/08/negative-frequency/