MIMO

Receive diversity in AWGN

Krishna Sankar16 years ago12 years ago309 mins

Some among you will be aware that in a wireless link having multiple antenna’s at the receiver (aka receive diversity) improves the bit error rate (BER) performance. In this post, let us try to understand the BER improvement with receive diversity. And, since we are just getting started, let us limit ourselves to additive white Gaussian noise (AWGN) channel (i.e assume that the channel gains are unity).

Single receive antenna case

Let us begin with the discussion with one transmit antenna, sending signals with energy $E_b$ and one receive antenna. Since we are considering only BPSK modulation, the signals which are sent out are either $+\sqrt{E_b}$ or $-\sqrt{E_b}$ . Let there be a single receive antenna having a thermal noise (aka AWGN) with mean $\mu=0$ and variance $\sigma^2 = \frac{N_0}{2}$ .

The probability density function of noise is,

$p(n) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(n-\mu)^2}{2\sigma^2}$ .

The received signal is of the form,

$y=x+n$ , where

$y$ is the received symbol,
$x$ is the transmitted symbol (taking values $+\sqrt{E_b}$ ‘s and $-\sqrt{E_b}$ ‘s) and
$n$ is the Additive White Gaussian Noise (AWGN).

From our discussion on BER for BPSK modulation in AWGN, we know that probability of bit error is,

$P_b=\frac{1}{2}erfc\left({\sqrt{\frac{E_b}{N_0}}}\right)$ .

Receive diversity with two antennas

Now consider the case where we have two receive antennas each having thermal noise (aka AWGN) with mean $\mu=0$ and variance $\sigma^2 = \frac{N_0}{2}$ . As the noise on each antenna is independent from each other, in signal processing parlance, we can say that noise on each antennas are i.i.d i.e independent and identically distributed. The transmitter is still sending symbols with energy $E_b$ .

The received signal is of the form,

$\left[\begin{eqnarray}y_1 \\ y_2 \end{eqnarray}\right] =x+\left[\begin{eqnarray}n_1\\n_2\end{eqnarray}\right]$ , where

$y_1$ , $y_2$ are the received symbols from receive antenna 1, 2 respectively,
$x$ is the transmitted symbol (taking values $+\sqrt{E_b}$ ‘s and $-\sqrt{E_b}$ ‘s) and
$n_1$ , $n_2$ is the Additive White Gaussian Noise (AWGN) on receive antenna 1, 2 respectively.

For simplicity, let us assume that the signal $+\sqrt{E_b}$ was transmitted. At the receiver, we now have

$y_1=\sqrt{E_b}+n_1$ and

$y_2=\sqrt{E_b}+n_2$

To decode, the simplistic (and the optimal in this scenario) is to take the mean of $y_1$ , $y_2$ and perform hard decision decoding, i.e

$y_s=\frac{y_1+y_2}{2}$ and if $y_s \ge 0$ implies the transmitted bit is 1 and $y_s \le 0$ implies transmitted bit is 0.

Now let us find out if there is any receive diversity gain by performing this averaging. Splitting $y_s$ into signal term and noise term

$\begin{eqnarray}y_s&=&\frac{\sqrt{E_b} + n_1 +\sqrt{E_b}+n_2}{2}\\&=&\sqrt{E_b}+\left(\frac{n_1+n_2}{2}\right)\end{eqnarray}$ .

The first term in the above equation is the signal term – which still transmit symbols with energy $E_b$ . The second term is mean of two Gaussian noise terms.

(a) From the discussion on sum of Gaussian random variables,

if $X$ is a Gaussian random variable with mean $\mu_1$ , variance $\sigma_1^2$ and $Y$ is another independent Gaussian random variable with $\mu_2$ , variance $\sigma_2^2$ , then $X+Y$ is another Gaussian random variable with $\mu_1 + \mu_2$ , variance $\sigma_1^2 +\sigma_2^2$ .

(b) Furher, from the discussion on functions of Gaussian random variables,

if $X$ is a Gaussian random variable with mean $\mu_1$ , variance $\sigma_1^2$ , then $aX+b$ is another Gaussian random variable with mean $a\mu_1 +b$ , variance $\left(a\sigma_1\right)^2$ .

Using the above two equations, the noise term $\frac{n_1+n_2}{2}$ is another Gaussian random variable with mean $\mu =0$ and variance $\sigma^2 = \frac{N_0}{4}$ .

When compared with the single antenna case, we can see the variance of the noise term is scaled by a factor of 2. This implies that the effective bit energy to noise ratio in a two receive antenna case is twice the bit energy to noise ratio for single antenna case.

$\left[\frac{E_b}{N_0}\right]_{eff,2}=\frac{2E_b}{N_0}$ .

So the bit error probability for two receive antenna case is,

$P_b=\frac{1}{2}erfc\left({\sqrt{\frac{2E_b}{N_0}}}\right)$ .

Expressing in decibels, with two receive antennas, we need only $10\log_{10}(2) = 3dB$ lower bit energy $E_b$ ! No wonder people like receive diversity. 🙂

Receive diversity with N receive antenna

With a general N receive antenna case, the received symbol is,

$\left[\begin{eqnarray}y_1 \\ y_2 \\ \vdots\\y_N\end{eqnarray}\right] =x+\left[\begin{eqnarray}n_1\\n_2\\ \vdots\\n_N\end{eqnarray}\right]$ , where

$y_1$ , $y_2$ ,… $y_N$ are the received symbols from receive antenna 1, 2 respectively,
$x$ is the transmitted symbol (taking values $+\sqrt{E_b}$ ‘s and $-\sqrt{E_b}$ ‘s) and
$n_1$ , $n_2$ ,… $n_N$ is the Additive White Gaussian Noise (AWGN) on receive antenna 1, 2,… N respectively.

For demodulation, we compute $y_s$ which is the mean of all the N received symbols, and if $y_s \ge 0$ implies the transmitted bit is 1 and $y_s \le 0$ implies transmitted bit is 0.

The variance of the noise term $\frac{\left(n_1 + n_2 + \cdots + n_N\right)}{N}$ is $\frac{\sigma^2}{2N}$ .

Effective bit energy to noise ratio in a N receive antenna case is N times the bit energy to noise ratio for single antenna case.

$\left[\frac{E_b}{N_0}\right]_{eff,N}=\frac{NE_b}{N_0}$ .

So the bit error probability for N receive antenna case is,

$P_b=\frac{1}{2}erfc\left({\sqrt{\frac{NE_b}{N_0}}}\right)$ .

Simulation Model

Simple Matlab/Octave example simulating a BPSK transmission and reception in AWGN only scenario with multiple receive antennas. The script performs the following

(a) Generate random binary sequence of +1’s and -1’s.

(b) Add white Gaussian noise on the received symbol on all the receive chains

(d) Perform hard decision decoding and count the bit errors

(e) Repeat for receive chains = 1, 2, 3, 4 for multiple values of $\frac{E_b}{N_0}$

(f) Plot the simulation and theoretical results.

Click here to download Matlab/Octave script for BER of BPSK in AWGN with receive diversity

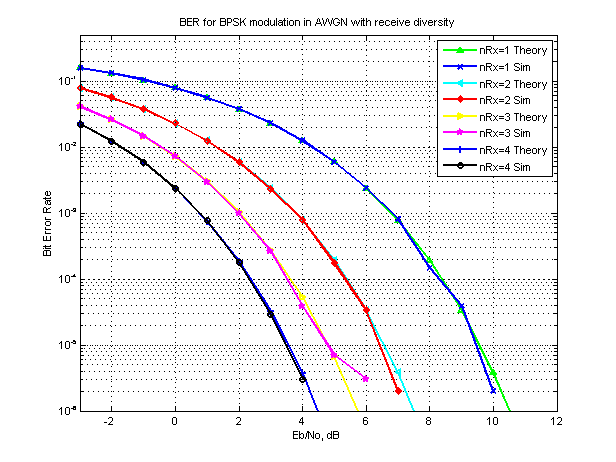
Figure: BER for BPSK in AWGN with receive diversity (number of receive antennas = 1, 2, 3, 4)

Observations

1. As desired, the simulation results show good agreement with theory.

2. With an N receive antenna system, the gain compared to single receive antenna case is around $10\log_{10}(N)$ . For example in the above figure, for bit error rate of $10^{-4}$ ,

with two receive antennas the required $\frac{E_b}{N_0}$ is 3dB lower,
with three receive antennas, the required $\frac{E_b}{N_0}$ is 4.7dB lower and
with four three receive antennas, the required $\frac{E_b}{N_0}$ is 6dB lower.

Hope this helped you get started with receive diversity. If not, please do drop in a comment. Happy learning.

30 thoughts on “Receive diversity in AWGN”

mazaismo says:

July 17, 2012 at 11:22 pm

what is the MATLAB code of BER performance of coherent FSK,PSK and QPSK

Reply
1. Krishna Sankar says:
  
  July 23, 2012 at 4:39 am
  
  @mazaismo:
  a) FSK @
  https://dsplog.com/2007/08/30/bit-error-rate-for-frequency-shift-keying-with-coherent-demodulation/
  b) QPSK/4-QAM@
  https://dsplog.com/2007/11/06/symbol-error-rate-for-4-qam/
  
  Reply
Ahmed says:

April 21, 2012 at 1:05 pm

Hi Krishna
I wonder if we consider Rayleigh fading channel, and suppose the received signals are
y1=h1*s+n1 and y2=h1*s+n1
How can you show the diversity order.
Or suppose we combine the signals with MRC y = w1*h1*s+w1*n1 + w2*h2*s+w2*n2
One more question, I don’t understand why we take the expectations of y1 and y1.
Thanks in advance

Reply
1. Ahmed says:
  
  April 21, 2012 at 1:58 pm
  
  Sorry y1=h1*s+n1, y2=h2*s+n2
  
  Reply
2. Krishna Sankar says:
  
  April 23, 2012 at 5:22 am
  
  @Ahmed: The post on Maximal Ratio Combining (MRC) with h1 and h2 being Rayeligh faded discuss the effective SNR and BER.
  https://dsplog.com/2008/09/28/maximal-ratio-combining/
  Hope that helps.
  
  Reply
arjun says:

March 20, 2012 at 12:24 am

sir can you please provide me with a valid code for the receiver in Ofdm.. it is very urgent and your help is needed..
thank you for the entire information that you have shared till now..

Reply
1. Krishna Sankar says:
  
  March 21, 2012 at 5:04 am
  
  @arjun: Please check posts in https://dsplog.com/tag/ofdm/
  
  Reply
Aishwarya says:

March 17, 2012 at 9:14 pm

can we use receiver Hard Decision Decoding if we have QPSK signal for same case. for e.g
ip = (2*(rand(1,N)>0.5)-1) + j*(2*(rand(1,N)>0.5)-1);
s = (1/sqrt(2))*ip;
If yes, please give the matlab equation (for ipHat) for all other condition being same as above. please try to reply as soon as posible.

Thank you.

Reply
1. Krishna Sankar says:
  
  March 18, 2012 at 11:31 am
  
  @Aishwarya: it should be straightforward for you to extend this to QPSK case
  
  Reply
  1. Aishwarya says:
    
    March 19, 2012 at 2:02 pm
    
    But in case if Qpsk it has imaginary part also in ip. and if we find real(yHat), then the error in the imaginary part will not be counted. so it may not find all the errors. Isn’t it?
    can you give the equation how can we perform hard decision decoding with both real and imaginary part taking into consideration.
    
    Reply
    1. Krishna Sankar says:
      
      March 21, 2012 at 5:05 am
      
      @Aishwarya: Yes, for QPSK we need to take both real and imaginary parts. Some posts discussing QPSK can be found at
      https://dsplog.com/2008/07/08/compare-bpsk-qpsk-4pam-16qam-16psk-64qam-32psk/
      https://dsplog.com/2012/01/01/symbol-error-rate-16qam-64qam-256qam/
      
      Reply
Sujith says:

October 26, 2010 at 7:09 pm

Hello Mr.Pillai

How to do equalisation if you are working on same program using rayleigh channel.

thank you

Reply
1. Krishna Sankar says:
  
  November 15, 2010 at 2:32 am
  
  @Sujith: There are couple of different ways. We can do Equal gain combining, Selection Diversity, and Maximal Ratio Combining (MRC). The MRC is optimal. Have discussed about each scheme @
  https://dsplog.com/tag/diversity/
  
  Reply
atlanta says:

July 26, 2010 at 11:24 am

hello sir,
i am trying to write a matlab code to calculate the BER of a DPSK modulation scheme for a rayleigh/ AWGN. So i need your help.
thank you sir…
i am waiting for your reply

Reply
1. Krishna Sankar says:
  
  July 27, 2010 at 7:11 am
  
  @atlanta: Please refer to the post on Coherent Demodulation of DBPSK
  https://dsplog.com/2007/09/30/coherent-demodulation-of-dbpsk/
  
  Reply
mahsa says:

August 1, 2009 at 2:28 am

hi
im trying to write a matlab code which i have 2 Tx and 1 Rx with fading channel, and AWGN noise and QPSK, i already wrote 1Tx and 1 Rx the BER for one Tx and 1Rx is correct acording to figures , but in the diversity form i should get less BER that i dont get, the problem is that i think my SNR has some problems , the one that i wrote is 1-10*log10(m)-10*log10(frame_pulse)) 1 is my snr, m is the length of time multiply by bandwidth i dont know what should i add more, thanx if you can help me
mahsa

Reply
1. Krishna Sankar says:
  
  August 5, 2009 at 5:47 am
  
  @mahsa: Unless you do some ‘special’ processing at the transmitter, sending the same information from both the 2 transmit antennas does not result in diversity gain. Please refer to the post on transmit beamforming
  https://dsplog.com/2009/04/13/transmit-beamforming/
  
  Reply
anuradha says:

June 3, 2009 at 9:21 pm

hi
i wanted to know few things……. about

Script for computing the BER for BPSK modulation in AWGN channel with receive diversity
what is the hard decision decoding and why it is used whether there is any alternative for that,,,,

second why that linewidth is used explanation for the same

graph is not proper for diff snr range as i tried
pls ans fast

Reply
1. Krishna Pillai says:
  
  June 7, 2009 at 2:09 pm
  
  @anuradha: My replies
  1/ Well, we need to use soft decision, if we are passing the output of demodulation to some other block (like a Viterbi decoder and so on). Otherwise, hard-decision is optimal.
  2/ Did you mean the linewidth option used in plot() function. This is just for controlling the width of the line used in the plot 😉 Type help plot for further details.
  3/ As you may be aware, your question is vague to say the least…
  4/ Sorry, I was traveling. Hence the 3-4 days of delay in my response.
  
  Reply
Khan Baba says:

June 3, 2009 at 3:47 pm

I hope that u r fine and doing well. can u plz tell me how SNR = Eb/N0.

Reply
1. Ashwini says:
  
  June 4, 2009 at 12:26 pm
  
  Check this link, Eb/No is explained in detail and most sufficient explanation till date, also some post on wirelesscafe.wordpress.com regarding SNR
  
  Eb/No link
  http://sss-mag.com/ebn0.html
  
  Reply
  1. Krishna Pillai says:
    
    June 7, 2009 at 2:13 pm
    
    @Ashwini: Thanks for the link.
    In WirelessCafe, you (and your team) have posted nice contents. I have bookmarked for future read. Keep up the good work. Hopefully, we can figure out of some ways to network and reach a wider audience in future.
    
    Reply
2. Krishna Pillai says:
  
  June 7, 2009 at 2:05 pm
  
  @Khan Baba: Well, SNR need not be equal to Eb/N0… 🙂 For bit more details, you may refer to the link http://sss-mag.com/ebn0.html
  (thanks to Ashwini).
  
  Reply
wayan says:

June 1, 2009 at 7:13 am

hellow Mr krishna
can you help me to make a matlab subscrip for BER QPSK with rain attenuation
thanks

Reply
1. Krishna Pillai says:
  
  June 7, 2009 at 1:52 pm
  
  @wayan: I am not familiar with modeling rain attenuation. However, I have written a post on symbol error rate for QPSK in AWGN
  https://dsplog.com/2007/11/06/symbol-error-rate-for-4-qam/
  
  Hope this helps.
  
  Reply
azhu says:

March 9, 2009 at 8:40 pm

but your SNR is for a signal branch, in practice, total SNR should be considered, if that, no improvement for diversity. am i right?

Reply
1. Krishna Pillai says:
  
  March 21, 2009 at 6:48 am
  
  @azhu: Hmm… no. Given that the transmit power is the same, as we add more receive antennas, we get improvement in SNR too. May I know why you think otherwise.
  
  Note: In the above example, as its BPSK Eb/N0 = SNR
  
  Reply
jimmy says:

February 13, 2009 at 5:25 am

Hi, is there any reference text that shows this Pb=1/2 erfc(sqrt(NEb/N0)) that I can find?

As we can reduce the ber significantly just by adding a few more antennas, may I know what are the assumptions make for this ber prove?

Thank you

Reply
1. Krishna Pillai says:
  
  February 20, 2009 at 5:48 am
  
  @jimmy: Please look at the post on BER for BPSK modulation in AWGN
  https://dsplog.com/2007/08/05/bit-error-probability-for-bpsk-modulation/ for the derivation of Pb=1/2 erfc(sqrt(NEb/N0))
  
  Assumed that the each receive antenna presents independent thermal noise.
  
  Reply
Pingback: Maximal Ratio Combining (MRC)