Negative Frequency

Last week, I received an email from Mr. Kishore. He was wondering about the physical significance of negative frequency. Does negative frequency really exist?

Though I have seen conflicting views on the net (thread in complextoreal.com, thread in comp.dsp), my perspective is that negative frequency exist. The concept of negative frequency helps me a lot to understand single sideband modulation (SSB), OFDM systems, I Q modulators etc (to name a few).

Simple explanation for negative frequency

The wiki entry on negative frequency provides a simple explanation using $cos(\omega t)$ as an example.

We know that $cos(\omega t) = cos(-\omega t)$ . This means the sign of $\omega$ cannot be un-ambiguously found out from observing $cos(\omega t)$ alone. This implies that it is reasonable to think that $cos(\omega t)$ has frequency components at both $\omega$ and $-\omega$ .

Similarly, this ambiguity exists for $sin(\omega t)$ too.

$sin(-\omega t) = -sin(\omega t) = sin(\omega t + \pi)$

Negative frequency using Taylor’s series expansion

Thanks to the nice paper by Mr. Richard Lyons, Quadrature Signals: Complex but not Complicated, Richard Lyons.

Let us first define the magic number $j=\sqrt{-1},\ j^2 = -1,\ j^3 = -j,\ j^4 = 1$ and so on.

The Taylor series expansion of $e^x$ , $cos(x)$ and $sin(x)$ are as follows.

$e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots$

$cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} -\frac{x^6}{6!} + \ldots$

$sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} -\frac{x^7}{7!} + \ldots$

Let us now define the Taylor series expansion of $e^{jx}$ .

$\begin{eqnarray}e^{jx}&=&1 + jx + \frac{(jx)^2}{2!} + \frac{(jx)^3}{3!} + \frac{(jx)^4}{4!} + \frac{(jx)^5}{5!} + \frac{(j6)^6}{6!} + \frac{(jx)^7}{7!} + \ldots\\ & = & 1 + jx - \frac{x^2}{2!} - j\frac{x^3}{3!} + \frac{x^4}{4!} + j\frac{x^5}{5!} - \frac{x^6}{6!} - j\frac{x^7}{7!} + \ldots\\ & = & \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} -\frac{x^6}{6!} + \ldots\right) + j\left(x - \frac{x^3}{3!} + \frac{x^5}{5!} -\frac{x^7}{7!} + \ldots \right)\\ & = & cos(x) + jsin(x)\end{eqnarray}$ .

Similarly,

$\begin{eqnarray}e^{-jx}&=&1 - jx + \frac{(-jx)^2}{2!} + \frac{(-jx)^3}{3!} + \frac{(-jx)^4}{4!} + \frac{(-jx)^5}{5!} + \frac{(-j6)^6}{6!} + \frac{(-jx)^7}{7!} + \ldots\\ & = & 1 - jx - \frac{x^2}{2!} + j\frac{x^3}{3!} + \frac{x^4}{4!} - j\frac{x^5}{5!} - \frac{x^6}{6!} + j\frac{x^7}{7!} + \ldots\\ & = & \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} -\frac{x^6}{6!} + \ldots\right) - j\left(x - \frac{x^3}{3!} + \frac{x^5}{5!} -\frac{x^7}{7!} + \ldots \right)\\ & = & cos(x) - jsin(x)\end{eqnarray}$ .

Combining the above two equations, one may write

$cos(x) = \frac{1}{2}\left(e^{jx} + e^{-jx}\right)$

$sin(x) = \frac{1}{2j}\left(e^{jx} - e^{-jx}\right)$ .

If we apply $x=2\pi f_o t$ , then we get,

$cos(2\pi f_ot) = \frac{1}{2}\left(e^{j2\pi f_ot} + e^{-j2\pi f_ot}\right)$ and

$sin(2\pi f_ot) = \frac{1}{2j}\left(e^{j2\pi f_ot} - e^{-j2\pi f_ot}\right)$ .

This forms the proof that a real sinusoidal having frequency $f_o$ is comprised of a complex sinusoidal having a positive frequency at $+f_o$ and a negative frequency at $-f_o$ .

Simple Matlab example for Negative frequency

Click here to download Matlab/Octave code for plotting the spectrum of real and complex sinusoidal

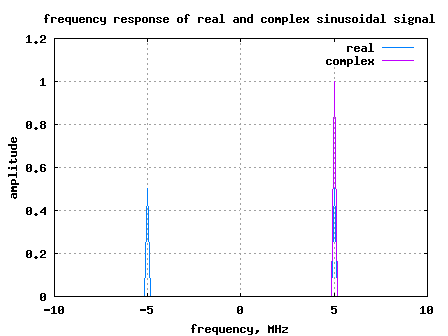
Figure: Spectrum plot showing positive and negative frequency

As discussed above, the real sinusoidal has frequency components at +5MHz and -5MHz where as the complex sinusoidal has frequency component only at +5MHz.

Negative frequency in OFDM

Some of you might be familiar with the IEEE 802.11a specification where subcarriers from [-26 to -1 and [+1 to 26] are used. The subcarriers -26 to -1 corresponds to usage of negative frequency and lets try to understand it.

The equation for an OFDM transmission is,

$\begin{eqnarray}s(t) =\frac{1}{\sqrt{T}}\underbrace{\sum_{0}^{K-1}a_ke^{\frac{j2\pi kt}{T}}}\ w(t) \end{eqnarray}$ ,

where

(a) $k=0,1,\ldots,K-1$ correspond to the frequency of the sinusoidal and

(b) $w(t)=u(t)-u(t-T)$ is a rectangular window over $[0\ T)$

(d) each information signal $a_k$ is modulated on to a complex sinusoidal having frequency of $\frac{k}{T}$ .

(e) Sum of all such modulated sinusoidals are added and the resultant signal is sent out as $s(t)$ .

In the IEEE 802.11a specification, symbol duration $T$ is 3.2 $\mu s$ , sampling frequency $f_s$ is 20MHz and $K=64$ .

The frequencies used for modulating the $a_k$ ’s are $\frac{0}{T}$ , $\frac{1}{T}$ , $\frac{2}{T}$ , $\frac{3}{T}$ and so on till $\frac{K-1}{T}$ . Expressing in Hz, this corresponds to frequencies from 0Hz, 312.5kHz, 625kHz, 937.5kHz, 1.25MHz,…, 10MHz, 10.3125MHz,… till 19.6875MHz.

From our understanding of sampling theory, we know that with a sampling frequency of $f_s$ , we can only see frequencies from $-\frac{f_s}{2}$ to $+\frac{f_s}{2}$ .

Note: The frequency $+\frac{f_s}{2}$ is called the Nyquist frequency.

So in our 802.11a example, what will happen to frequencies which are modulated on subcarriers lying from 10MHz till 19.6875MHz?

Quick answer: They get folded!

The frequencies from 10MHz till 19.6875MHz gets folded and seems as if they are lying from -10MHz to -312.5kHz.

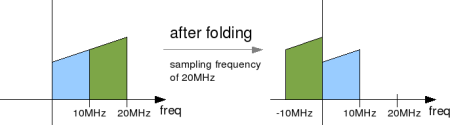
Figure: Spectrum folding to negative frequency in IEEE802.11a specification

Further, folding of the spectrum to the negative frequency region does not cause any problems. Reason: $a_k$ ’s which where modulated on complex sinusoidals having frequencies from 0 till 10MHz did not have any negative frequency component.

Note:

In general, one can say if a sinusoidal is of frequency $f$ is sampled with a frequency $f_s$ and if $f>\frac{f_s}{2}$ , the frequency $f$ gets folded to a frequency $f-Nf_s$ within $\left[-\frac{f_s}{2},+\frac{f_s}{2}\right)$ , where $N$ is an integer.

The concept of folding is well explained in Chapter 1.4.1 of [DSP: PROAKIS]. A simple example of folding which we may see in our day to day life is with a ceiling fan. One may see that the blades of the fan are rotating at a slower speed in a direction opposite to the actual rotation of the fan blades. Needless to say that the sampling frequency of our eye’s are not good enough.

Happy learning.

Reference

[DSP: PROAKIS]: Digital Signal Processing, John G. Proakis

Quadrature Signals: Complex but not Complicated, Richard Lyons

Tagged as: frequency, OFDM

D id you like this article? Make sure that you do not miss a new article by subscribing to RSS feed OR subscribing to e-mail newsletter. Note: Subscribing via e-mail entitles you to download the free e-Book on BER of BPSK/QPSK/16QAM/16PSK in AWGN.

{ 11 comments… read them below or add one }

1 Arturo November 14, 2008 at 9:19 pm

A minor typo, after the line: “Combining the above two equations, one may write”; the sine equations must have a minus sign instead of a plus sign when the sine is expressed as the addition of the two exponentials

2 Krishna Pillai November 15, 2008 at 8:46 am

@Arturo: Thanks for the close review. I corrected the equation.

3 Sergio January 29, 2009 at 1:34 am

All the events in the real world are real but frequently an easly mathematical description may be gived using mathematical entity like complex numers.
For example a modulation like M-PSK is realized like a superposition of two real signals (sin plus cosine) but rather than use in your formulas two (real) numbers you may compact your notation using a single complex number and is implied to take the real part.
The link between real and complex trigonometric functions is gived from the eulero formula.This formula say that cos(x)=(1/2)[exp(ix)+exp(-ix)] and sin(x)=(1/2i)[exp(ix)-exp(-ix)].
Using the various theorems about Fourier trasforms every function with finite Fourier integral are descriptable like a super position of sin and cos of opportune amplitude, frequency and fase.
So the negative frequency component is pureli a collateral effect of the complex description.

4 Krishna Pillai January 30, 2009 at 5:47 am: @Sergio: So, are you saying that negative frequency is a mathematical notion? However, I think negative frequency do exisit (as -ve numbers do exist) .

5 pulkit September 1, 2009 at 12:17 am

just we know the concept of -ve frequency is sometimes used to distinguish a decreasing angle from an increasing one why we need the negative frequencies in fourier transforms

6 Krishna Sankar September 7, 2009 at 5:31 am: @pulkit: Sorry, was that a question or a statement?

7 vedika September 14, 2009 at 11:42 pm

inputiFFT(subcarrierIndex+nFFTSize/2+1) = ipMod(ii,:);

how does the above expression work? what is the use of : (colon) ?
why do we have to use the following expression?
–subcarrierIndex+nFFTSize/2+1

And please let me know
how the cyclic prefix has been done?

8 Krishna Sankar September 18, 2009 at 5:36 am: @vedika:
1. For each row ii, am assigning all columns of ipMod to the variable inputiFFT per the indexing subcarrierIndex+nFFTSize/2+1
2. For inserting cyclic prefix, we take the last 16 samples from the ifft output and pad it to the same variable again.
% adding cyclic prefix of 16 samples
outputiFFT_with_CP = [outputiFFT(49:64) outputiFFT];

9 Kokulan September 28, 2009 at 7:16 am

Hi Mr Krishna Sankar!
I know that Negative frequencies exist but I just have a question: why negative frequencies are needed in the spectrum?

10 Krishna Sankar October 1, 2009 at 5:23 am: @Kokulan: The negative frequencies helps us to understand, for example, IQ modulation.

11 vivek January 28, 2010 at 5:30 pm

if i say that spectrum is between -f and f,then does it mean that power in the spectrum will be distributed equally on both sides?

Negative Frequency

Simple explanation for negative frequency

Negative frequency using Taylor’s series expansion

Simple Matlab example for Negative frequency

Negative frequency in OFDM

Reference

Related posts

Subscribe

Categories

Archives

Top Rated posts

Recent Posts

Comments

DSP

FPGA

General