The article gives a quick overview of a simple statistical multipath channel model called Rayleigh fading channel model.
Multipath environment
In a multipath environment, it is reasonably intuitive to visualize that an impulse transmitted from transmitter will reach the receiver as a train of impulses.
Figure: Impulse response of a multipath channel
Let the transmit bandpass signal be,
, where
is the baseband signal,
is the carrier frequency and
is the time.
As shown above, the transmit signal reaches the receiver through multiple paths where the path has an attenuation
and delay
. The received signal is,
.
Plugging in the equation for transmit baseband signal from the above equation,
.
The baseband equivalent of the received signal is,
,
where is the phase of the
path.
The impulse response is,
.
Rayleigh fading model
The phase of each path can change by radian when the delay
changes by
. If
is large, relative small motions in the medium can cause change of
radians. Since the distance between the devices are much larger than the wavelength of the carrier frequency, it is reasonable to assume that the phase is uniformly distributed between 0 and
radians and the phases of each path are independent (Sec 2.4.2 [WIRELESS-COMMUNICATION: TSE, VISWANATH]
).
When there are large number of paths, applying Central Limit Theorem, each path can be modelled as circularly symmetric complex Gaussian random variable with time as the variable. This model is called Rayleigh fading channel model.
A circularly symmetric complex Gaussian random variable is of the form,
,
where real and imaginary parts are zero mean independent and identically distributed (iid) Gaussian random variables. For a circularly symmetric complex random variable ,
.
The statistics of a circularly symmetric complex Gaussian random variable is completely specified by the variance,
.
The magnitude which has a probability density,
is called a Rayleigh random variable.
This model, called Rayleigh fading channel model, is reasonable for an environment where there are large number of reflectors.





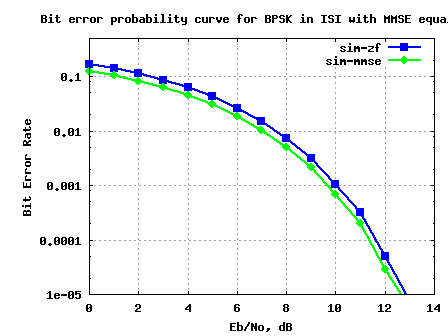
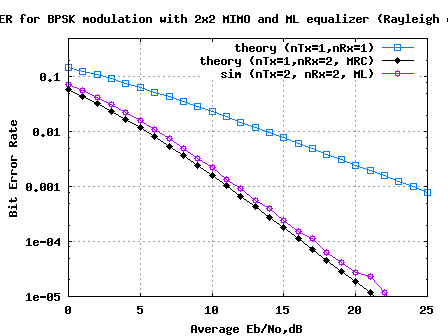
i doing project on V_BLAST, and don,t have relevant theory and codes on v-blast .I need ur help sir please send what is V_BLAST? and relevant codes
@jagadeeswara reddy: please check the post
https://dsplog.com/2009/04/21/six-equalizers-for-v-blast/
sir, can u please explain what is V-BLAST in your words.
@jagadeeswara reddy: Well, that’s a difficult ask. Hope the following pointers will be of help.
http://en.wikipedia.org/wiki/Bell_Laboratories_Layered_Space-Time
https://dsplog.com/2009/04/21/six-equalizers-for-v-blast/
Hello,
i just want to ask that is there any relation between AWGN noise variance and offset in Wireless signals like OFDM.
@Aman: The noise, caused by the random motion of electrons, is characteristic of the device and is independent of the modulation.
Discussion on thermal noise is posted at
shebyhttps://dsplog.com/2012/03/25/thermal-noise-awgn/
Hope this helps
Hello Sir,
Can you explain me about the STBC frequency selective fading channel.
Please Sir Send me the matlab codes for STBC for multitap channel. I need the codes very urgently.
Thank you very much Sir
With Kind Regards
@jyoti: When STBC is coupled with OFDM, then the multipath channel becomes independent flat fading channel for each subacarrier.
Some STBC related posts are at:
https://dsplog.com/tag/stbc/
Few OFDM with multipath Rayleigh channel related posts are at:
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
https://dsplog.com/2012/01/01/symbol-error-rate-16qam-64qam-256qam/
Thanks , Can I have the matlab code?
@maherjassem: Please check out posts under https://dsplog.com/category/channel/
Can you tell me how to calculate the frequency response and coherence bandwidth of a time invariant channel
@Guman: Frequency response can be found using a fft() or equivalent tool to capture the frequency domain information. From the frequency response, one can look at the profile define the coherence bandwidth.
@Krishna: Thank you very much for your informative articles.
I have few questions slightly related to this article. I need your opinion on how you would have approached this scenario. This scenario is hypothetical.
Specification:
Assume I have to design a communication system for a specific area and specific purpose. My customer specified me minimum BER (QoS) and transmit power. I have liberty to choose rest (for eg: delay, modulation, complexity).
Approach:
Now I have to choose modulation technique, error correction algorithm. This depends on, what channel and bandwidth is.
As it is specific place, I don’t know how channel looks like . I would have approached this way,
Step 1: Measure and model channel:
Assume I am able to measure channel. Find PDF of the channel somehow.
Using this PDF, I can find outage probability or Bit error rate.
Step 2: To meet this BER, choose modulation technique and error correction algorithm.
Step3: Decide how much Sync you need, based on Channel.
Step 4: Start design and test back.
My question is Q1: How to measure real time channel if I don’t have built communication system?
Q2. Is my approach is right?
Q3. If I am right, have I overlooked something.
Thank you very much.
I am waiting for your inputs.
With regards,
Abhijith Gopalakrishna.
@Abhijith:
Nice. One would also need to look at the range requirement of the communication link. To start off, assuming a free-space path loss model, transmit power and receiver noise bandwidth one can get a good estimate for the range.
Now depending on whether the system is going to be indoor or outdoor, the free-space path loss model needs to be tweaked. Doing a channel measurement in the target deployment environment is definitely a good idea, however it may be expensive and time consuming. Alternately, one can look at typical channel models available in the literature and pick one which can closely match your desired use case. Hope this helps.
Mr.Krishna
How can we relate SNR with (or in terms) path loss model?
@Thoyagi: That should be straight forward.
Pt : transmit power in dBm
Pr : received power in dBm
NF : noise floor in dBm (bandwidth -174+10*log10(BW_mhx*1e6) and implementation dependent)
Pr = Pt – PathLossdB
SNRdB = Pr – NF
hi mr. krishna, I need your help please in CDMA multipath Rayleigh fading by MATLAB .
@musaab: sorry, i have not posted anything on CDMA till date in the blog.
hello Krishna
I’m simulating a rayleigh channel but I’m difuculdades the following question. I would estimate the attenuation of each path, eg
h = [1 0 0 0.2 0 0 0 0.4];% multipath channel with three taps (as has already been quoted here)
Simulation is not yet a rayleigh model. I believe it is the constant h that the data are already convoluidos that is fixed by h.
In simulation rayleigh OFDM BPSK attenuation could be inserted in this format
h = [1 0 0 0.2 0 0 0 0.4] for exempo
or
randn should be generated for real and imaginary Simulation adequate?
Thanks for the help.
@Paulo: Depends on what is your expectation from the simulations.
Hey! Why do you divide with 20 in this expression:
y = h.*s + 10^(-Eb_N0_dB(ii)/20)*n;
isn’t it supposed be divided by 10?
@filip: It’s the scaling for the noise voltage signal
HELLO SIR,
i am trying to use ”rayleighchan” inbuilt function in matlab 7.11,but it gives me following error… Undefined function or method ‘channel.rayleigh’ for input arguments of type ‘double’.
Error in ==> rayleighchan at 116
chan = channel.rayleigh(varargin{:});
actually i want to construct one doppler object….for that i need this rayleighchan function…..can u plz help me out…..
THANKS A LOT…..
@tejashree: Sorry, I do not have Matlab installed
Hi Krishna,
I need MATLAB programs to determine the error probabilities for orthogonal signalling by employing Hard decision and Soft decision decoding.
Would you please guide me
@Hemavathi: Bit error rate for BPSK in AWGN is discussed at
https://dsplog.com/2007/08/05/bit-error-probability-for-bpsk-modulation/
For hard decision vs. soft decision as an input to Viterbi decoder,
https://dsplog.com/2009/01/14/soft-viterbi/
hello sir, im currently working on ofdm tx and rx.i have succesfully written the code.but i want to do it in rayleign multipath fading channel.would you mind to tell me what parameters i hav to consider and how to implement it. thankyou sir
@ramireddy: Maybe the post on BER for BPSK in OFDM with Rayleigh channel helps you
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
The aim of the project is to investigate the performance of BPSK and (QPSK) modulation schemes in Rayleigh fading channels using Monte Carlo simulations.
Consider the following discrete signal model for BPSK modulation
y(i)=α(i) x(i)+w(i) i=1,2,…
where x is the transmitted signal, α is the channel coefficient (Rayleigh distributed), and w is the zero-mean additive white Gaussian noise (AWGN).
Generate a large vector of the random input signal x (assuming uniform distribution) using bipolar representation of 0’s and 1’s.
Generate a large vector of the channel coefficient α realizations. Show the match between the obtained distribution and the theoretical one (as given in 5.49 in the text book).
Generate a large vector of the AWGN noise realizations for different values of the noise variance (σ_n^2). Show the match between the obtained distribution and the theoretical Gaussian distribution.
Implement, in MATLAB, to obtain the received signal y (using as sample from the generated vectors above for each iteration). The channel power has to be unity.
Implement the detector as a simple threshold detector and the compute the average bit error rate (BER). Remember to accumulate at least 50-60 errors for each BER value. Plot the resulting BER versus the signal to noise ratio (SNR) in dB. The range of SNR should be from 0 to 30 dB. Compare the obtained curve to the one in fig. 6. 53 in the textbook (or use eq. 6.156).
@ahmed: You can refer to the post on BER for BPSK in Rayleigh channel
Hiii, I want to tell immense thanks to owner of this dsplog for such a good nd helpful hand towards sharing knowledge.
I personally felt to show my feelings here that my field is Communication and doing MS in the same field, as while doing my work I get some problem and when no any book can help in finding the solution certainly my mind clicks me abt this blog to get the solution and actually I get it every time even in the simplest nd fully understandable way.
Thanks for such a nice contribution.
@preeti: Thanks much
Sir, i have a doubt in 802.22 basics. It tells, due to switch over from analog tv tx to digital tv tx , lot of white spaces are available. WRAN devices sense this white space and use it.
My question is where we need to locate the Customer premises equipment for sensing the white space.? (i.e. we need to locate CPE at every home.?..)
And i think most of the TV broadcasters in india move to DTV. so obviously lot of white spaces are there…then why we need to sense and fix some time period for sensing …etc…
Plz…plz..reply…i am not sleeping for the couple of days…i could not find the answer in google and books…plz help me.. and reply as early as possible….
@hasnee: I guess FCC has some new rulings on usage of TX white space, and the bunch of documents can be found under
http://www.fcc.gov/Document_Indexes/Engineering_Technology/2010_index_OET_Order.html
under FCC-10-174
Hi Krishna,
Do you have any topic related to Rician Fading Channel? I am doing assignment and want to know more about analytical equation for Rician. Tks.
@Rebecca: Not discussed anything on Rician channel
Thank you sir
your suggested article and Coding related to PDF of rayleigh fading channel helped me very much …… Thank u again sir……..
Sir, one problem is there with me is that i want to generate wavelets of signal at tx side in order to send via multipath rayleigh channel….
I dont know how to apply wavelet transform on signal at tx as i have already used bpsk on tx part…
Sir plzzzzz help me… give me some way to generate wavelets on this tx signal..
@Aman: I am not familiar with wavelets
Thanks for the explanation. Shouldn’t the Rayleigh pdf be [z/sigma^2]*exp[-z^2/(2*sigma^2)] ? You have written it as sigma^3 for the first term.
@Sandeep: Thanks for noticing the typo. I corrected it.
Dear Krishna… Do u know how to implement rayleigh high doppler channel in the ofdm system? Please help me
U r doing good work. Keep it up.
Pushpa
@Pushpa: With high doppler, the channel will be time varying. I have not tried modeling that case, hence unable to provide you a simulation code….
Hi Krishna,
Please i which to ask that how can i model a two ray equal power channel model with delay spread between adjacent paths. I am considering delay spread of 5 and 40 microseconds between adjacent paths.
Please if you have any code on this i will appreciate your help .
Thank you.
@Ilesanmi: For a two ray channel, create channel with two taps with same amplitude. Insert appropriate number of zeros between the taps as per your sampling time definition.
Hi Krishna,
I would very thankful if you could also help me with my question like you have helped so many people here.
I am trying to implement a SRRC pulse shaping for QPSK modulated scheme in MATLAB. Filter length = 21 taps long. Filter type: Single tapped delay line filter.
Looking forward to your reply.
Thanks,
Nikita
@Nikita: You can have a look at some posts on transmit pulse shaping
https://dsplog.com/2008/04/22/raised-cosine-filter-for-transmit-pulse-shaping/
https://dsplog.com/2008/05/01/eye-diagram-plot-matlab-raised-cosine-filter/
https://dsplog.com/2009/05/08/ber-with-matched-filtering/
Hi Krishna,
Thank you very much for your prompt response and links to the relevant discussions.
Previously, I have simulated the Raised Cosine pulse shapes and received them using the matched filter receiver. I have also plotted the raised cosine pulses and verified it with the eye diagram.
I am getting stuck while implementing SRRC pulse.
There was a post by someone in one of the discussions seeking help for the error in code but it wasn’t answered in great detail.
It would be great if you could help. This is really important.
Thanks,
Nikita
@Nikita: If you are able to get the raised cosine thing up, then getting root raised cosine simulation might be reasonably simple.
Did you try to implement the equation for root raised cosine
http://en.wikipedia.org/wiki/Root-raised-cosine_filter
OR
even simpler, you can use the Matlab functions for raised cosine and root raised cosine
Filtering with Raised Cosine Filters
http://www.mathworks.com/access/helpdesk/help/toolbox/comm/ug/fp69291.html
All the best
respected sir
You are doing an excellent work. Are u conducting a course or course material on matlab.
What’s your understanding on beamforming,
Thanks a lot sit
@E.S.Shajahan: Thanks.
a) Not conducting course on Matlab
b) https://dsplog.com/2009/04/13/transmit-beamforming/
Hi,
I am trying to related the number of Tap of Rayleigh fading with its RMS delay spread.
kmax = ceil (5*tau/Ts);
profile = exp(-(0:kmax)*Ts/tau);
profile = profile/(sum(profile));
channel = sqrt(profile/2).*(randn(size(profile))+j*randn(size(profile)));
I found this code somewhere online and does this help?
For OFDM the symbol duration, TS = 4us and im looking at tau(rms delay spread) = 75ns. In the end, i only get 2 Taps. Is this correct?
@Bala: Well, I recall that with a channel with 75ns RMS delay spread, the taps can go even upto 0.8us. Please refer to the Naftali channel model
a) http://www.commsdesign.com/article/printableArticle.jhtml?articleID=16505977
b) https://mentor.ieee.org/802.11/file/00/11-00-0282-00-00sb-evaluating-the-performance-of-ieee802-11-hrb-proposal-in-multipath.ppt
I would like to know if there is an option to import results from matlab to open WNS for simulation purpose. If yes how. Thanks in advance
@Geethu: Sorry, am not aware
Hi Krishna,
Thank you very very much
If the channel became Nakagami-m multipath fading channel,How to present this type of channel.
Thank you again
@Ahmed: Sorry, I have not tried modeling Nakagami channels
Dear Krishna,
when i am doing the simulation of the rayleigh channel.I choose the formula r(t)=sum[ an(t)*x(t-tau(t))].
My question is how can i generate the attenuation an(t)?
Best regards,
@Jun: Sorry, did not understand your query
Hello krishnan sir
Could you kindly send me some code where there are multiple users and each is assigned a signature waveform(DS-CDMA). I need this is study the BER of such system.
Awaiting ur reply.
Thanks in advance
Krishnan Sir,
can u tell me how to do channel estimation for OFDM System with pilot symbol intoduced . The pilots are introduced in block type. The channel estimation has to be done by LS method.
Dear Krishna
In your post you said theta(n)=2*pi*fc*Tao(n) is the phase of the nth path; what does it mean? is it the phase delay introduced by nth path? If so then how can we say that? I mean we know the overall delay introduced by all paths is basically the phase response but how can we say it to individual path?
Thanks
Anser
I wanted to know regarding how can i model a GMSK modulation over two path rayleigh channel, in matlab using rayleighchan command, and also reg BER calculation & plot.I am new to matlab and i am unable to demodulate my signal after passing it through rayleigh channel.
Hello Krishna Pillai I am student doing my thesis I have one problem it looks like you have discuss about it. but I am not clear . the problem is about computing SNR value base on distance using Erceg model for pathloss can it be SNR=Pt+Gt+Gr-PL-Rs where Pt is transmitted power, Gt is the antenna gain Gr is the receiving antenna gain PL is the pathloss and Rs is the receiver sensitivity (which comprises of themal noise, noise figure etc) ?
thanks in advance
@Dahiru: Yes, the equation is correct.
Hi Krishna Pillai
Iam Waleed from Palestinian
I was in need the LMS bemforimg for pre-FFT and Post-FFT processing OFDM communiation system
Thank for all
@waleed salos: Sorry, I have not discussed LMS beamforming.
Hello,
thank you for sharing your knowledge. I have one question. How about in case of using Nakagami environment for QPSK modulation . how to implement simulation ?
thanks
with BR
@gulmira: Sorry, I have not tried modeling Nakagami channel.
hye krishna
i need to ask that how can i pass my signal through a rayleigh channel, i am comparing the ofdm QAM signal performance by passing it through awgn, rayleigh and racian channel.
can you help me with that. i have an ofdm i simple pass it through awgn channel and analyzed it by its command in matlab.
now i need to pass that signal with the rayleigh and racian channel as well to visualize.
plz help me with that.
@hassan: The post on BER for BPSK in OFDM modulation with Rayleigh multipath channel might be of help
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
can u plz tel me where m wrong
thanks in advance
hi krishna m working on mimo ofdm so far i have worked on ofdm with 2/3 convo rate coding with qpsk….but when i pas it through rayleigh channel the result is 0.5 ber..i applied mlse equalizer it does work fine QPSK (with no ofdm) . but with ofdm same thing gets 0.5 BER..plz telme where m wrong…
my rayleigh channel is
chcoeffs = [.986 .845 .237 .12345+.31i]; % Channel coefficients
filtmsg = filter(chcoeffs,1,msg); % Introduce channel distortion.
tblen = 10; % Traceback depth for equalizer
chanest = chcoeffs; % Assume the channel is known exactly.
msgEq = mlseeq(filtmsg,chanest,const,tblen,’rst’) % Equalize
then demodulation n then viterbi decoding
@Mak_m: Is it working with OFDM, but without channel? Further, I do not see the code, for taking the fft at the receiver.
I can’t understand the sentence: relative small motions in the medium can cause change of 2 pi radians. Since the distance between the devices are much larger than the wavelength of the carrier frequency, it is reasonable to assume that the phase is uniformly distributed between 0 and radians and the phases of each path are independent……..
ellaborate and explain the defintion of Rayleigh fading channel………
@kalidoss: I was trying to mention that phase of Rayleigh faidng channel can vary anywhere from 0 to 2pi radians uniformly.
Dear Krishna,
Can you give me any guidance with using MRC for a case for once receiver and multiple transmitters…. I am using the model where the received signal after the combiner is :
Ym = conj(h1)* y1 + conj(h2)*y2 ……
But the performance for this diversity channel comes to be worse than one without diversity, I hope you shed some light on this, or advise an algorithm in line with your Simulations with flat fading channels.
@Ali Habeeb Ahmad: When you have multiple transmit antennas, one might want to do pre-processing at the transmitter to ensure that the signals combine coherently in the receiver. I have written a brief post on Transmit beamforming @
https://dsplog.com/2009/04/13/transmit-beamforming/
Hope this helps.
Hello Dear Krishna, I am designing a sphere decoder for MU-MIMO. I have coded one MIMO sphere decoder but I got difficuilty in calculatin the BER for the sphere decoder in Rayleigh fading channel, can you please help me in this matter plz. Thanks
@Adnan: I have not tried modeling sphere decoding, but I would guess one would want to get the performance close to Maximum likelihood. Are you observing 0% BER with no-noise case?
Hi Krishna,
That BER in AWGN is really nice! i really like it. Do you have Matlab script for computing Bit Error Rate with Binary FSK in Rayleigh channel? I need to write the code for my project. Can you make to send me?
thank you alots!
@hugh: Sorry, I do not have code for Binary FSK in Rayleigh channel. However, you may look up the post on BER for binary FSK in AWGN channel as a reference.
https://dsplog.com/2007/08/30/bit-error-rate-for-frequency-shift-keying-with-coherent-demodulation/
Hi Krishna,
you are good at the channel to BER. Can I ask if add two AWGN channels togeter in the FSK? it is significate to analysis the signal performance. if so, what results will come out?
thank you!
@hugh: Did not quite follow your question. Did you mean, you want to double the noise power? If so, the BER will degrade by around 3dB
Hi Krishna,
Maybe the comment is a little bit off-topic but I’m quite desperate.
I’m writing a thesis to provide with some MIMO capabilities the network simulator OpenWNS.
I program a non-gemoetrical matrix channel generator (also knowed as H). To generate this matrix we only need two parameters, number on antenas (Tx and Rx) and correlation factor. Several papers talk about that the MIMO gain deppends on the correlation factor of the channel matrix.
The generator works quite good giving matrix with correlations between 0 and 0.6.
Then we transform the SISO stream in MIMO Stream with the next formula:
SINRk=(SINRsiso/#antennas)*(1/diagonal of the inverse of (H^H*H))
This formula provide us K post-processing SINR. But when I calculate the gain with the different correalations is always more or less the same, and I don’t know where is the fail/problem.
Sorry if it’s disturbs you, but I don’t know what else can I do.
Thank you in advance.
Charly
After several analisis the problem should be in the channel matrix generator.
The function to generate the the desired correlated channel is the next one:
function result = Rayleigh_Ch(Corr_param,N, n_samples)
%Corr_param=Correlation parameter desired between 0 and 1
%N=Number of correlated variables (ex: in a 4×4 channel matrix
%N=4×4=16)
n_t=sqrt(N);
n_r=sqrt(N);
Wrayl=zeros(n_t,n_r,n_samples);
RaylValue=zeros(n_t,n_r);
rayl_param=sqrt(2/pi);
%Matrix Initialization
V_Complex=zeros(N,n_samples);
W=zeros(N,n_samples);
%%%%
%% STEP 1: NORMALIZE THIS MATRIX TO CREATE THE NORMALIZED COVARIANCE MATRIX
%% OF RAYLEIGH SAMPLES
%%%%
Kg=Corr_param*ones(N,N);
for pos_diag=1:1:N
Kr(pos_diag,pos_diag)=1;
end
%%%%
%% STEP 2: GENERATE N UNCORRELATED COMPLEX GAUSSIAN SAMPLES IN VECTOR V,
%% THEN DETERMINE THE COLORING MATRIX L AND GENERATE THE COMPLEX GAUSSIAN
%% SAMPLES USIN W=L*V
%%%%
%obtaining the coloring matrix
[L,P,U]=lu(Kg);
%GENERATE N UNCORRELATED COMPLEX GAUSSIAN SAMPLES IN VECTOR V
for sample=1:1:n_samples
%generate correlated complex Gaussian samples using W=L*V
V_Complex(:,sample)=sqrt(0.5)*randn(N,1)+1i*sqrt(0.5)*randn(N,1);
W(:,sample)=L*V_Complex(:,sample);
end
Wgauss=reshape(W,1,N*n_samples);
%%%%
%% STEP 3: Create the desired Rayleigh envelopes
%%%%
Wrayl=abs(real(Wgauss))+1j*(imag(Wgauss));
Wrayl=reshape(Wrayl,4,4,n_samples); %every sample is a rayleigh fadding channel matrix
result=Wrayl;
end %end of the function
I obtain the Rayleigh distribution from the gaussian one, making the real part absolute and then accopling the imaginary part.
Hope it will help.
@Charly: I guess, you are expecting to see that post processing SNR will be low when the correlation is high, but not able to see that. To debug, may I suggest that you try computing with two channel matrices of 2×2 dimenstion
(a) [1 1; 1 -1] : orthogonal channel,
(b) [1 1 ; 1 1] : channel with rank of 1,
Yes, that is the point. I don’t know what is missing in the channel matrix deffinition.
I will try to change the code to work with 2 antennas at the receiver and transmissor side (matrices of 2×2).
Any suggestion for the correlated channel generation?
Thank you for your fast reply.
Charly
@Charly: Sorry, I have not tried modeling correlated channel. Good luck in your explorations.
Than you anyway for your attention.
nice work…
plz include flat fading modeling and Fading Effects due to Doppler Spread…and other statistical models as clarke’s Model etc and techniques to combat this.
@kangkan: Sure, adding posts on Doppler channel is in my mind for some time. Need to do it… .:)
@ krishna
thanx for ur reply
yea i agree….
but tell me do we have to u phase lock loop or any other phase detection loop in case of complex rayleigh channel or an lms equalizer would server the purpose????
regards
sara
@sara: Well, the assumption in the above post is that there is no frequency offset and the only distortion is the effect of the channel. If there is frequency offset, we need to have mechanism for removing it (like PLL) prior to equalization
Hi Krisha,
Hope you are doing well. Can you please mail me the link for performance analysis of MIMO in Rician Fading channel. Thanks.
@Mustafa: Sorry, I have not tried modeling Rician fading channel
hi krishna!
greetings,
all these statements presented above is extreamly helpful to me, and i resently am trying to simulate a paper in which it needs to entry the circularly symmetric gaussian r.v.,could u help me to code the program?
thanx in advance!
@ lee_john: A circulary symmetric gaussian random variable has real and imaginary components having independent Gaussian distributions.
N = 10^4;
rv = randn(1,N) + j*randn(1,N);
Hope this helps.
thanx alot krishna….
ur efforts are really helpful…
can u plz tell me how the behaviour of real single tap rayleigh chaneel differs from complex single tap raleigh channel.???
regards
sara
@sara: In the case of a real channel, only the amplitude is affected. With a complex channel, both amplitude and phase are affected, agree?
chào ngài,tôi đang làm mô phỏng OFDM,điều chế QAM trong multipath(rayliegh), làm thế để tái tạo lại được chòm sao QAM?
@jenifer: Can you please translate your query to english.
for avgpow=0.01:0.025:1
const = pskmod([0:4-1],4)
x=randint(1,100,4); % generating symbols
tx=pskmod(x,4);
scale=modnorm(const,’peakpow’,avgpow);
%*******transmitted signal**************
mod_sig=scale*tx;
%*******SIGNAL1**************
snr1=randint(1,1,[-5,10]); % to generatge random value of snr in each iteration
y1=awgn(mod_sig,snr1);
%*******SIGNAL2**************
snr2=randint(1,1,[-5,10]);
y2=.34*awgn(mod_sig,snr2);
hd = dfilt.delay(2); % add a delay of 2 samples in its input
y2 = filter(hd,y2);
%*******SIGNAL3**************
snr3=randint(1,1,[-5,10]);
y3=0.127*awgn(mod_sig,snr3);
hd = dfilt.delay(4);
y3 = filter(hd,y3);
final_sig=y1+y2+y3;
y_rcvd=final_sig/scale;%unscale recieved signal
rcv_data=pskdemod(y_rcvd,4);
[err ,ber] = biterr(rcv_data,x)
result(k,1)=avgpow;
result(k,2)=ber;
k=k+1;
end
plot(result(:,1),result(:,2),’g’)
this is my code in which i want to use equaliztion at the receiver , i have tried a few inbuilt equalizers but the worsen the results
@sara: Sorry, due to time constraints, may I decline to debug the code. Further, I do not have most of the functions which you have used here (i use Octave for my simulations – do not have matlab).
From a quick googling, I found the example from Mathworks
Adaptive Equalizer Simulation (Part I) This script simulates a communication link with PSK modulation, raised-cosine pulse shaping, multipath fading, and adaptive equalization.
http://www.mathworks.de/products/featured/embeddedmatlab/demos.html?file=/products/demos/shipping/comm/adapteqpt1.html
Hope this helps.
hi krishna!
hope you must be fine…..
ur posts are really helpful for me
i am having a small problem
i am trying to simulate a multipath enviornment in AWGN channel by introducing delay in the signals
but at the receiver i am gettin quite high BER
can u kindly suggest me how to equalize these multipath signals at the rcvr in order to reduce BER
@sara: How are you equalizing for the effect of the channel. In general, if you are introducing a channel h(t) in the received signal, at the receiver you should introduce a filter g(t) in the receiver such that g(t) convolved h(t) is an impulse.
Hello ..
Well I am doing a project on ultra wideband system.I have done my simulation for AWGN channel.Now,I want to add rayleig channel to my transmiited data.Can you plz tell me the matlab code for generating rayleigh fading.
Thanks
@Rizwan: The Rayleigh channel modeling which I use are typically single tap (flat fading) Rayleigh channel. If you want to generate a multipath channel with each tap randomly distributed, you may use
nTap = 10;
ht = 1/sqrt(2)*1/sqrt(nTap)*(randn(1,nTap) + j*randn(1,nTap));
hi Krishna,I get a hard time in implement the MMSE linear equalizer (non-adaptive) can you help me please..thanks.
@jawad: Please refer to the post on MIMO with MMSE equalizer.
https://dsplog.com/2008/11/02/mimo-mmse-equalizer/
i am working on channel simulation in wireless communication can i get your help
for my research
Prof nataraj
thanks and regards
@nataraj: I have not worked much on channel modeling. Most of my simulation were assuming flat fading Rayleigh channel. However, yes we can discuss.
Dear Krishna i hope you are doing fine … i am simulating an OFDM system … i obtained the curves for BER without the introduction of any channel model … now I want to run my simulations by introducing a PROAKIS B CHANNEL … but the problem is i dont have much idea of this model…can you kindly give me an overview or helpful resource from where i can get an idea about this channel? and how can i simulate it in matlab …
i shall be very grateful
@invizible: Sorry, I do not have references for Proakis channel model. The closest I found is that its a 3 tap rayleigh channel (from here)
One may also look at Naftali channel model
can u send me the rayleighb fadind channel matlad simu codes
can give d code for rayleigh fadind channel model
@Syed: You may look @ the code in the post
https://dsplog.com/2008/07/17/derive-pdf-rayleigh-random-variable/
Hi sir
I want to simulate measures in the time in a static receiver and I need to know how us the “raylrnd function” in MATLAB.
I don’t understand The Help in MATLAB because I get big numbers.
Also I think the “lognrnd function” is more easy to use so it is correct to use the “lognrnd function” instead of the “raylrnd function” in MATLAB?.
P.D Sorry for my spelling mistakes. Thank you
@jorge: To model Rayleigh channel, I typically use a complex Gaussian noise
h = 1/sqrt(2)*(randn(1,N) + j*randn(1,N)).
From a quick googling obtained the following links about raylrand
(a) raylrand help page in Mathworks
(b) http://www.dsprelated.com/showmessage/260/1.php
From (b), “raylrnd function implements “abs(randn(1,N)+j*randn(1,N))” for sigma =1 instead of
abs(sqrt(0.5)*(randn(1,N)+j*randn(1,N))).”
Hope this helps.
Then another thing krishna,is it possible to go for blind channel estimation using LS technique?,it would b very helpful if you can clarify on this as i am stuck up in the middle of proj phase
@akram: Sorry, I have not worked on blind channel estimation.
Sorry, I forget to put some code.
To simulate the fadding I use this code:
ray = (raylrnd(b, n_r, n_t) + sqrt(-1) * raylrnd(b, n_r, n_t)) / sqrt(2);
Where n_r/n_t is the number of receive/transmit antennas (to generate the matrix) and b is the sigma of the rayleigh distribution.
The definition of the command raylrnd is:
R= raylrnd(B,m,n) returns a matrix of random numbers chosen from the Rayleigh distribution with parameter B, where scalars m and n are the row and column dimensions of R.
I don’t know what B parameter I need to put.
Thanks
Hi Krishna,
I’m making some simulations in Matlab (trying to obtain a MIMO SNR stimation from a SISO SNR, without any geometrical information).
I make the assumption than we where indoor and the channel can be modeled like a Rayleigh distribution. After check several codes all the people is making a channel Matrix (H) with the rand function, what about the raylrnd function?
I’m trying with this function but I don’t know what sigma I need to use. You can help in find this value? (or any idea to get 4 diferent SNR streams (4×4 MIMO) from one SNR stream (SISO).
Thank you in advance
@Charly: In the simulations, which I did, I defined a flat fading Rayleigh channel comprised Gaussian distributed real and imaginary components. h = 1/sqrt(2)*(randn(1,N) + j*randn(1,N)).
The 1/sqrt(2) factor helps to make the variance of h as unity.
Since I do not have Matlab, I do not have the function raylrand. However, from a quick googling obtained the following links:
(a) http://www.mathworks.com/access/helpdesk/help/toolbox/stats/index.html?/access/helpdesk/help/toolbox/stats/raylrnd.html
(b) http://www.dsprelated.com/showmessage/260/1.php
From (b), “raylrnd function implements “abs(randn(1,N)+j*randn(1,N))” for sigma =1 instead of
abs(sqrt(0.5)*(randn(1,N)+j*randn(1,N))).”
Hope this helps.
hi sir
i am doing channel estimation using pilot tone in ofdm system– i wrote the code for estimation– and i used rayleigh fadding
ray=randin(1,n_tab)+j*randin(1,n_tab);
now i have to introduc the doppler shift
i.e — d= doppler frequncy/subcarrier spacing; doppler shift=exp(j*2*pi*d);
is it correct? and i have to plot BER vs various doppler frequncy — BER GET WORSE WHEN DOPPLER FREQUNCY IS MORE — IS THERE ANY DIFFERNCE BW DOPPLER SHIFT AND DOPPLER SPREAD — and i used exponential power delay profile A= exp(-k/10) k=0:L-1;
L =CHANNEL PATH — I USED IN TIME DOMAIN — AND I USED CONV(OFDM_SIGNAL ,A) — IS IT COORECT OR I HAVE TAKE FFT AND MULTI WITH FREQ DOMAIN
Hi thiruppathi,
You are designing a time-variant..
Rayleigh fading channel is time-variant channel…
How can you convolute if you are using time invariant channel..
It’s just my doubt…
hi sir
I used block and comb type pilot pattern to estimate the channel;
so i have coded like this
for i:sb(1)%sb(1)=numberof ofdmsysmbols
chan=randin(1,n_tab)+j(randin(1,n_tab)
xht = ofdm_symc(i,:);
xht=conv(ht,xht);
end
is it correct?
@Thiruppathi: Infact you do need to do convolution for each ofdm symbol. You can take the full vector (which is the concatenation of several ofdm symbol) and convolve that with channel ht.
@thiruppathi: My replies:
1. Am not familiar with modeling doppler. Hence not commenting.
2. Yes, BER getting worse with higher doppler frequency is expected 🙂
3. conv(ofdm_signal, channel) is correct.
thank you sir, i have one more doubt.
How to model a Rayleigh time varying fading channnel;
—
expontial power delay profile with rayleigh fading is
d=exp(-(1:L);L = number of paths
ray=d+i*d ;
is it correct?
@thiruppathi: Well, I think, to model time varying channel you might need to do multiple convolution on the packets. For eg, the first chunk of time you do convolutional with a channel, the for the next chunk of time, you convolute with another channel.
Thank you sir,
i have one more doubt — how to model the rayleigh time vaying fading in ofdm system ( time variation within ofdm symbol;
and
i have coded for this spcifications
channel =rayleigh,
expontial power delay tabs
d=exp(-(1:L) L- number of tabs
ray=d+j*d;
is it correct?
how to simulate the rayleigh with doppler
@thiruppathi: I have not written posts on modeling doppler effects. Maybe I should do. Will do so in future.
Hello sir,
I need some ideas about How to calculate Avrerage SNR per symbol for plotting SER Vs Average SNR in dB? Can you help me?
@Benzia: Average SNR per symbol can be set by measuring the power of signal and noise over large number of symbols. I have written a post on BER for BPSK in Rayleigh channel with OFDM modulation. The signal and noise scaling in the Matlab model accompanying the post should be helpful.
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
Hope this helps.
hi sir,
I doing project in channel estimation using block and comb type pilot pattern(ofdm_system).
i facing problem in introducing the channel effects
can you help me how to introduce the doppler effect and rayleigh fadding;
@Thiruppathi: I have not tried doppler, but I can provide you a pointer to Rayleigh fading.
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
In that post, I convolve OFDM transmission with a 10tap rayliegh channel and equalize for the channel and compute BER.
I assume that the channel is known at the receiver. In your case, you made do channel estimation and use the estimated channel for equalization.
hai,i am doing a blind channel estimation scheme for OFDM,can u suggest a good way and please suggest how to model the channel.Do we have to model using the impulse response form,and what is channel length?
@akram: Sorry, I have not worked on the problem of blind channel estimation. The multipath channel is typically modelled in the time domain – using impulse response. The shape of the impulse response and the duration of the impulse response depends on the environment under consideration.
I have written a few posts on Rayleigh channel @
https://dsplog.com/2008/07/14/rayleigh-multipath-channel/
https://dsplog.com/2008/07/17/derive-pdf-rayleigh-random-variable/
Hope this helps
Hello Krishna,i am not sure of channel length mentioned some in research papers,can you enlighten me on this aspect,and by ensuring length of c.p < channel length, ISI is avoided in OFDM,Is that so?
@akram: Yes, you are right. You may also look at the post BER for BPSK with OFDM in Rayleigh multipath channel.
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
In that post, the channel is a 10-tap rayleigh channel and the OFDM system has a cyclic prefix durtion of 16. As there is no-interference, the BER performance is comparable to a flat fading Rayleigh channel simulations.
i want a simple matlab programme to simulate pcm system 8-bites with gaussian channal and bit error rate please i need it very very quickly
@nebal: Sorry, I have not written posts on PCM systems.
Hola necesito ayuda, necesito simular un canal con diversidad MRC con L canales en el Receptor correlados con una mismaganancia promedio, donde el (Tcoherencia < Ttransmision), necesto representar la capacidad ergodica para L1, L4, L4., si me pueden ayudar………
GRACIAS…
aTTE. RICHARD
@Richard: Can you please translate the query.
Dear Krishna
Currently I do my thesis and will submit next week but until I still cannot plot rayleigh pdf apply to my model. My data measurement by array 121(11×11)points so how to plot?
I no have much skill for matlab so if you can guide me some or if possible write complete code to me that is good for me I dont know anyone more to help.
Thanks in advance
@Sun: You can mail me queries in the code if any. I do not prefer to write ‘complete code’ 🙂
Dear all,
Can u plz help me for the Jitter/Delay in AWGN/Rayleigh fading channel for adaptive modulation
regds
@mak: I did not understand your problem statement. Can you please elaborate more.
Hi Kirshna;
I need ur help in simulating MC-CDMA.
i create the channel as i early told u in this way.
when I used one Tap i can use zeroforcing method as u described.
but when second Tap is activated lets by putting P2=0.8
Then how i make equalization at receiver.
The code is as under:
x=transdata1; % MC-CDMA BPSK Data with
%———————-Channel——————————————-
taps=2;
p1=1;
p2=0;
gain1=sqrt(p1/2)*[randn(1,length(x)) + j*randn(1,length(x))];
gain2=sqrt(p2/2)*[randn(1,length(x)) + j*randn(1,length(x))];
n=1:length(x);
delay1=1;
delay2=2;
for n=delay1+1:length(x)
x1(n)=x(n-delay1);
end
for n=delay2+1:length(x)
x2(n)=x(n-delay2);
end
transdata=gain1.*x+gain2.*x1
%————————Addition of noise ——————————-
noise = 1/sqrt(2)*[randn(1,length(x)) + j*randn(1,length(x))]; % Noise
snr = [0:10]; % multiple Eb/N0 values
ps=mean(abs(x).^2); % Power of the transmitted signal
for i = 1:length(snr)
y = transdata + (sqrt(3*ps)*10^(-snr(i)/20))*noise; %Addition of Noise
%————————————————————————-
%————————–Receiver —————————————
recdata=y;
L=length(y);
rx0=recdata.*conj(gain1); %Zeroforcing Equalization
%rx0 = 1./( gain1.*conj(gain1)+ 10^(-snr(i)/10)).*conj(gain1).*y; % mmse equalization
rx1=reshape(rx0,N,length(rx0)/N);
Krishna
I am trying to simulate IEEE 802.22 WRAN environment for my MSc project. Network consists of a WRAN BS with 50 CPEs spread randomly within its coverage area and a TV broadcast station located further away from the WRAN environment. My aim is to get the SNR of each of the 50 CPEs due to the signal (BPSK signal) from TV station. Channel is assumed to follow Rayleigh fading distribution. How to i do this preferably in MATLAB?
@Bwalya: From your problem statement, it seems like you are looking for finding the path loss from BS to each of the 50 CPE’s.
For doing that, you need to know the path loss exponent in the environement. Based on the transmit power and the path loss exponent, one can find the received power. Once the received power is known, based on the noise floor of each receiver (ideally depending on noise bandwidth), SNR can be computed.
The link in wiki on path loss might be helpful
http://en.wikipedia.org/wiki/Log-distance_path_loss_model
Hope this helps.
Thanks but i still have some concerns. My path loss exponent is say 3.8 but as the 50 CPEs are randomly distributed i cannot predict their distances from TV station, which are needed to get the received power for each CPE. How do i get around this? I prefer to use MATLAB.
@Bwalya: Maybe can you use rand() function to generate uniformly distributed random variables which is in a circle to generate the distance randomly. Small Matlab/Octave code snippet along with.
clear all; close all;
theta = 2*pi*rand(1,10^5);
mag = rand(1,10^5);
op = mag.*exp(j*theta);
plot(real(op),imag(op),’b.’)
The absolute value of op maybe used as representative of distance.
Hope this helps.
Thanks Krishna, your hint seems to have just opened my eyes. I’ll keep informed of the outcome.
Thank you sir.
Sir,
A small doubt:
CASE:
A time-invariant indoor wireless channel with LOS component at delay 23 ns, a multipath component at delay 48 ns, and another multipath component at delay 67 ns.
calculate the delay spread assuming
demodulator synchronizes to the LOS component. Repeat assuming that the demodulator synchronizes to the first multipath
component.
whether,
LOS component == first multipath component ?
@Ramya: In the case where demodulator synchronizes to the first multipath component, it means that we have significant energy from the pre-cursor (los component). I think, you need not treat LOS component == first multipath component. Treat it as a channel having both pre-cursor taps and post-cursor taps.
hi sir
— I have the problem in introducing the expontial power delay profile in ofdm system — and rayleigh fadding –can you help me — i am doing project in matlab
@Thiruppathi: For modeling channel model with exponential power delay profile, one may look at the Naftali channel model used in 802.11 communications. The article Modeling Multpath in 802.11 Systems should provide you more insights.
http://www.commsdesign.com/article/printableArticle.jhtml?articleID=16505977
https://mentor.ieee.org/802.11/file/00/11-00-0282-00-00sb-evaluating-the-performance-of-ieee802-11-hrb-proposal-in-multipath.ppt
For Rayleigh fading you may refer to the post,
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
thank you so much –it is helpful my work.
i eager to ask many questions , can I
@thiruppathi: Yes, you can. 🙂
need your help krishna please.
Hi, can i do it this way:
The cdf of rayleigh distribution is
F(h) = 1 – exp(-h^2/2sigma^2)
h = sqrt(-2sigma^2 * ln(1-F(h))
I am not sure how to obtain sigma^2, so in the matlab code, i set 2sigma^2 = 1.
h = sqrt(-log(rand(1,N)));
y = h.*s + 10^(-Eb_N0_dB(ii)/20)*n;
But i obtain the result which is different from yours. Is it possible to do it this way also? And how do we obtain sigma^2? Thank you
@jimmy: I do not think it is possible to find the random variable from the probability of the random variable. For eg, consider a simple uniform distributed random variable from 0 to 1. Its CDF is linear between 0 and 1, but it does not mean that we can find the random variable.
Maybe you would also want to check Box Muller transform
http://en.wikipedia.org/wiki/Box-Muller_method
Hope this helps.
Thank you for your response SIR
sir,
I was talking about BPSK BER simulation in AWGN channel.
I didnt mention it in my previous mesg.
sorry.
HELLO SIR,
I have seen the Script for simulating binary phase shift keyed transmission and reception and compare the simulated and theoretical bit error probability.
In that Matlab code i had small doubt.I the noise addition y = s + 10^(-Eb_N0_dB(ii)/20)*n; Why are U introducing 20 instead of 10 for converting Eb_No_db in db to ratioless quantity.(as power is dealt).
Waiting for your reply
thanks a lot in advance.
@ramya: The term Eb_N0_dB corresponds to the bit power over noise power. However when we are adding noise, we are adding the noise in the voltage domain (and not in the power domain). Hence to scale the noise voltage, we need to use 10^(-Eb_N0_dB(ii)/20). Hope this makes sense.
hello
i need the code of MIMO detection technique which is named as Zero Forcing ..plz
@Junaid: Please refer to the post
MIMO with Zero Forcing Equalizer
https://dsplog.com/2008/10/24/mimo-zero-forcing/
@rahul: Sorry, I have not yet tried to simulate Nakagami fading. Hopefully, the following link might be of use to you
Nakagami fading
http://wireless.per.nl/reference/chaptr03/ricenaka/nakagami.htm
All the best.
sir ..
i am working on ber calculation of ofdm channel through nakagami fading channel ..
do u have some matlab code for that..
or how to generate nakagami fading channel?
thanks in advance
@Abrar: That should be reasonably simple.
x1 = [x 0 0 ];
x2 = [0 x 0 ];
x3 = [0 0 x ];
The zero padding is done to ensure that the matrix dimensions are matching. Does this help?
hi i want to produce delay in signal as i have:
N=10^6; % Bits of data_user1
data_user1= rand(1,N)>0.5; % Generation of data user1
x=data_user1
fs=1
p1=1;
p2=0.2;
p3=05;
gain1=sqrt(p1/2)*[randn(1,length(x))+ j*randn(1,length(x))];
gain2=sqrt(p2/2)*[randn(1,length(x)) + j*randn(1,length(x))];
gain3=sqrt(p3/2)*[randn(1,length(x))+ j*randn(1,length(tx))];
y=gain1*x1+gain2*X2+gain3*X3;
where
x1=x
x2=x with one sample delay
x3=x with two sample delay
can u tell me how I generate X2 and X3.
how I put delay in signal.
Thanks and Take care
@Cheb Hosni: Thanks. 🙂
Sure, do send in your results.
you have done a great job thank you i try to improve some methods and i will send you the results
@Tahmid: Though I have not written on error rate with M-QAM channel, I can point you to
http://wireless.per.nl/reference/chaptr05/digimod/fadserah.htm
The second section of the post discuss SER for M-QAM in Rayleigh fading.
Hope this helps. Once I understand the equations, I may write an article on the topic.
Hi Krishna,
Have you managed to determine the BER performanve of M-QAM modulation over a rayleigh fading channel?
I understand the process of getting the BER for BPSK over the rayleigh channel, but get a bit lost when it comes to 4/8/16QAM. In particular I would like to know how to generate the coefficients and apply them to the signal.
thanks
@Lealem: Sorry for the delayed response.
Please check the reply @
https://dsplog.com/2008/08/10/ber-bpsk-rayleigh-channel/#comment-1151
I have seen the simulation code which u used to simulate a Rayleigh fading channel. But i would like u to ask a hit how to simulate a frequency selective Rayleigh fading channel for OFDM application. I think the above simulation out put is a flat Rayleigh fading.
Thank you!!!
@Lealem: Sure, please do post your question.
Hello! Krishna how are you today?
i just need a hint to simulate an OFDM over a time varing multipath fading fading channel(rayleigh), i have begin doing a simulation but i encounter a problem in the midle of my work. Can u please help me!
Thank you!
Thank you! for your response
@Lealem: This something which I am planning to do. Like we derived the BER for BPSK in AWGN channel, we will derive the BER for BPSK in Rayleigh fading channel and back it up with Matlab simulation scripts. This is something which I am planning to do with in the coming 7 days.
Hi Krishna
can you please help me how to plot the channel impulse response. I mean for varying delay how can we plot the power delay profile for channel impulse response in matlab?
@Ideal: Well, the most simplest example is
h = [1 0 0 0.2 0 0 0 0.4]; % multipath channel with 3 taps
plot(h);
If we assume that the sampling frequency of the taps is Ts, then the first and second tap are separated by 3Ts and the second and third tap are separated by 4Ts.
Does this help?
Hello! Sir
i have tried to read the Rayleigh fading channel model,but do you have a matlab code to simulate and test ,this fading channel over a wirelees environment.particularly QAM,16-QAM,
…..or Over an OFDM system.performanve of M-QAM modulation over a rayleigh fading channel(i.e SNR Vs BER).
Thank you!