(11 votes, average: 4.64 out of 5)
Loading ...
Let us derive the theoretical 16QAM bit error rate (BER) with Gray coded constellation mapping in additive white Gaussian noise conditions. Further, the Matlab/Octave simulation script can be used to confirm that the simulation is in good agreement with theory.
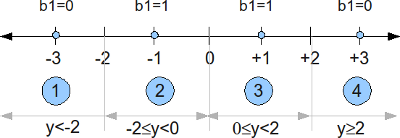
Gray coded bit mapping in 16-QAM modulation
As we discussed in the previous post on Binary to Gray code for 16QAM, the 4 bits in each constellation point can be considered as two bits each on independent 4-PAM modulation on I-axis and Q-axis respectively.
| b0b1 | I | b2b3 | Q |
| 00 | -3 | 00 | -3 |
| 01 | -1 | 01 | -1 |
| 11 | +1 | 11 | +1 |
| 10 | +3 | 10 | +3 |
Table: Gray coded constellation mapping for 16-QAM
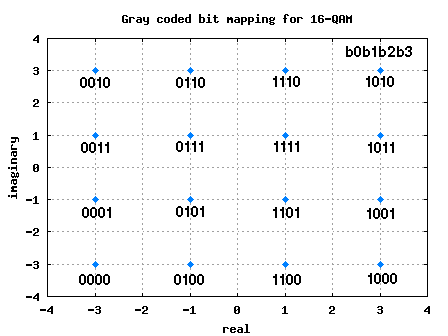
Figure: 16QAM constellation plot with Gray coded mapping
Symbol Error and Bit Error probability
As can be seen from the above constellation diagram, with Gray coded bit mapping, adjacent constellation symbols differ by only one bit. So, if the noise causes the constellation to cross the decision threshold, only 1 out of bits will be in error. So the relation between bit error and symbol error is,
.
Note:
For very low value of , it may so happen that the noise causes the constellation to fall near a diagonally located constellation point. In that case, the each symbol error will cause two bit errors. Hence the need for approximate operator in the above equation. However, for reasonably high value of
, the chances of such events are negligible.
Bit energy and symbol energy
As we learned from the post discussing Bit error rate for 16PSK, since each symbol consists of bits, the symbol to noise ratio k times the bit to noise ratio i.e,
where,
.
16QAM BER
From the post detaling the derivation of 16QAM Symbol error rate, we know that the symbol error is,
.
Combining the above two equations, the bit error rate for Gray coded 16QAM in Additive White Gaussian Noise is
Simulation model
The Matlab/Octave script performs the following:
(a) Generation of random binary sequence
(b) Assigning group of 4 bits to each 16-QAM constellation symbol per the Gray mapping
(c) Addition of white Gaussian Noise
(d) Demodulation of 16-QAM symbols and
(e) De-mapping per decimal to Gray conversion
(f) Counting the number of bit errors
(g) Running this for each value of Eb/No in steps of 1dB.
Click here to download : Script for computing 16QAM BER with Gray mapping
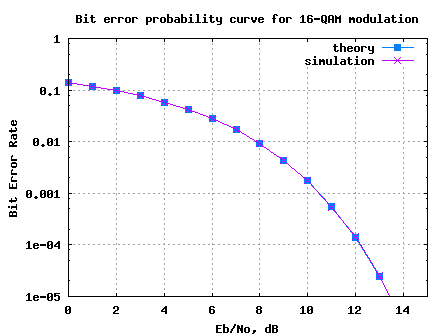
Figure: Bit Error Rate plot for 16QAM modulation with Gray mapping
I think we have analyzed the bit error and symbol error probabilites for most of the PSK and QAM modulation schemes in Additive White Gaussian Noise. Time to move on to error rate in multipath channel. receiver diversity. MIMO channel, modulation with memory etc etc 
Related posts
- Bit error rate for 16PSK modulation using Gray mapping
- Binary to Gray code for 16QAM
- Comparing 16PSK vs 16QAM for symbol error rate
- Softbit for 16QAM
- Comparing BPSK, QPSK, 4PAM, 16QAM, 16PSK, 64QAM and 32PSK
D id you like this article? Make sure that you do not miss a new article by subscribing to RSS feed OR subscribing to e-mail newsletter. Note: Subscribing via e-mail entitles you to download the free e-Book on BER of BPSK/QPSK/16QAM/16PSK in AWGN.
{ 59 comments… read them below or add one }
hi
I need article about walsh modulator
plz help me
bye
Hi, I have found your matlab code on the 16qam ber with gray code on the site http://www.dsplog.com and I have two question to ask you please.
1) What is the difference between “16qam ber with gray code” and “16qam ber without gray code”?
2) How do you get the theoretical expression of any M-aire qam ber.?
can you give me the corresponding expression of the 64-qam.?
Thanks for your help.
@yvon: My replies:
1/ With Gray coded mapping, the bit loading into adjacent constellation symbols differ by only one bit. So, each error in constellation symbol typically results in one bit being in error. Without Gray coded bit mapping, this assumption is no longer true.
2/ I have posted about theoretical derivation of M-QAM symbol error rate @
http://www.dsplog.com/2008/05/24/article-in-dspdesignlinecom-m-qam-symbol-error/
Hope this helps.
Hello Krishna Pillai
Your blog helps me a lot!
I still have some question about the BER and SER on 16QAM
In code for caculating SER
n = 1/sqrt(2)*[randn(1,N) + j*randn(1,N)];
y = s + 10^(-Es_N0_dB(ii)/20)*n; % additive white gaussian noise
In code for caculating BER
n = 1/sqrt(2)*[randn(1,N) + j*randn(1,N)];
y = s + 10^(-Es_N0_dB(ii)/20)*n; % additive white gaussian noise
1)what’s the difference using Es/N0 or Eb/N0?
2)if I want to draw the curve of SER and using Eb/N0 as the x-axis
is that wrong??
Thanks~
@K.T.Liao: My replies:
1) Es/N0 refers to symbol to noise ratio and Eb/N0 refers to bit to noise ratio. For eg, in 16QAM, each constellation symbol carries 4 bits, so Es/N0 = 4Eb/N0.
2) Nothing wrong in plotting SER vs Eb/N0. I have written a post on it @
http://www.dspdesignline.com/howto/208801783;jsessionid=QJJFYXQLQJMO1QE1GHRSKHWATMY32JVN?pgno=2
hi i need the matlab code for
” channel estimation and predicition for adaptive OFDM links”.
plz help me….
@venkat: Sorry, I do not have the Matlab code.
sir, i am new here. How i can add convolution encoding & viterbi decoding within the code. Are the code same for 16psk & 16qam???if u have code pls write.
@ipraz2: You can look at some convolutional encoder + Viterbi decoder posts @
http://www.dsplog.com/2009/01/04/convolutional-code/
http://www.dsplog.com/2009/01/04/viterbi/
http://www.dsplog.com/2009/01/14/soft-viterbi/
http://www.dsplog.com/2009/07/27/viterbi-with-finite-survivor-state-memory/
http://www.dsplog.com/2009/08/21/matlab-or-c-for-viterbi-decoder/
You may find 16PSK posts @
http://www.dsplog.com/2008/03/18/symbol-error-rate-for-16psk/
http://www.dsplog.com/2008/05/18/bit-error-rate-for-16psk-modulation-using-gray-mapping/
Good luck.
hi sir.
i’m new to matlab and have problem to modulate the 64QAM bit error rate.
how do i change the code u wrote in 16QAM to 64QAM or 256QAM?
every help is much appreciated.
@izzat: Please check the post http://www.dspdesignline.com/howto/207601769 and
http://www.dsplog.com/2008/07/08/compare-bpsk-qpsk-4pam-16qam-16psk-64qam-32psk/
Hello ! Thank you so much for this great work ^_^
I have a question about the n noise :
n = 1/sqrt(2)*[randn(1,N) + j*randn(1,N)]; 0 dB variance
if I didn’t use a complex noise, wh
Hello ! Thank you so much for this great work ^_^
I have a question about the n noise :
n = 1/sqrt(2)*[randn(1,N) + j*randn(1,N)]; 0 dB variance
if I use a real noise, what is the value of the variance ?
@Fritzou: 3dB less.
@Fritzou: If you dont use complex, then the variance will be down by 3dB.
I dont understand why while normalizing the transmit power to 1, you use the factor 1/sqrt(10). Would you explain it more? How about this factor in 32QAM and 64QAM? Thank you
@minh: Please refer http://www.dsplog.com/2007/09/23/scaling-factor-in-qam/
Thanks for the great info on here, it’s helping alot…
I am having a problem seeing how I would factor in the number of users, and the processing gain, of a CDMA system for the Probability of Bit error….
I am assuming that the Gp and the number of users, would be factored into the value for Eb but I’m not sure. Can you give me some direction on this?
Thanks
@Preston: Well, I did not quite understand how you are using 16QAM Gray mapping to the CDMA case? In the CDMA case, I would expect you to have a code for each user.
Hello Mr Krishna Sankar
Great work
why you didn’t use an filter in the transmission and in the reception?(raised cosine)
what would I do if I had this case ?
Thanks .
@Fritzou: The transmit and receive filters will cause additional notational complexity, which I wished to avoid in this post. I have some posts on simulations with transmit and receive filters
a) http://www.dsplog.com/2008/05/01/eye-diagram-plot-matlab-raised-cosine-filter/
b) http://www.dsplog.com/2008/04/22/raised-cosine-filter-for-transmit-pulse-shaping/
c) http://www.dsplog.com/2009/05/08/ber-with-matched-filtering/
please send me simulation for 16QAM and 64 QAM modulation and demodulation for convolutionaly encoding and viterbi decoding and theoritical BER for convolutionaly BPSK,QPSK,16QAM,64QAM
@shadat: Please refer to the post
http://www.dsplog.com/2008/07/08/compare-bpsk-qpsk-4pam-16qam-16psk-64qam-32psk/
http://www.dsplog.com/tag/viterbi
I am waleed from palestinian
I was in need the performnce of bit error rate in pre-ffT and postfft at frequency selective fading .
plesae help me
thank for all
@waleed salos: Hopefully the post on BER for BPSK with OFDM in multipath channel might be of help
http://www.dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
Dear Krishna sankar
I waleed salos Thank alot for Reply but I need Matlab codes for Post and pre-FFT Beamforming in an OFDM system
or
LMS Beamforming for Pre and Post-FFT processing in OFDM communication systems
Thank for all
@waleed: Sorry, I am not familiar with the topic which you are referring to.
hye sir…. do you have any tutorial on how to structure the constellation because the symbols is randomly being plot in the graph… i want to start with {0000} first and lastly to {1111)..- from left top corner of the constellation then move to the right and down…
@anna: If you see carefully, its not chosen randomly. Its chosen in a way such that adjacent constellation symbols differ by one one bit (and that called Gray coding)
please help me in 16 qam modulation.any one send me the matlab code of 16 qam modulation.
@atif: Also check out http://www.dsplog.com/2007/12/09/symbol-error-rate-for-16-qam/
sir,
i am mid way in matlab.i mean not very good and not very bad.
i am simulating and implementing the practical adsl environment in matlab.
please help me regarding it.
@kanchan: All the best. You can ask your queries in the comments section
I want to realize the simulation of the transmission using OFDM with 16QAM thank you for helping me if possible as much as possible
@hassan: I have discussed BPSK in OFDM @ http://www.dsplog.com/2008/06/10/ofdm-bpsk-bit-error/
Hopefully, you can adapt the simulation in the above post for 16QAM case.
Dear Sir,
For BPSK AWGN AND BPSK RAYLEIGH , Eb = 1 already. But for 16-QAM, Eb=2.5 by doing theoretical calculation and also what you did in your 16-QAM script. Now how shall I make Eb=1 for 16-QAM case so that I can compare this 16-QAM with BPSK AWGN AND BPSK RAYLEIGH?
Please kindly help me in this above problem.
Thank You
@Hassan: To normalize the power for 16QAM constellation, scale it by 1/sqrt(10).
http://www.dsplog.com/2007/09/23/scaling-factor-in-qam/
pls send me ber for bpsk,qpsk,8qam,16qam,64qam. pls send me that matlab code
@sridhar: Plz look @
http://www.dsplog.com/2008/07/08/compare-bpsk-qpsk-4pam-16qam-16psk-64qam-32psk/
Hy . I think you might have some errors in your results. You have to divide your result by 2 otherwise when you have low SNR your error rate will be above 1.
https://controls.engin.umich.edu/wiki/images/c/c4/Table_Erf.pdf
Best regards,
Ovidiu
@Ovidiu: Are you sure?
Hello Sir,
I want to compare BER performance of OFDM system using BPSK, M-PSK and M-QAM schemes with Rayeleigh/Ricean Fading channel. Can u please send me script which can help me …..please I am new to MATLAB
@Ojasvi: You can symbol error rate for a general M-QAM in OFDM over AWGN at
http://www.dsplog.com/2012/01/01/symbol-error-rate-16qam-64qam-256qam/
Converting symbol error rate to Bit error rate should be relatively simple. You can refer to the 16QAM BER example at http://www.dsplog.com/2008/06/05/16qam-bit-error-gray-mapping/
Sir can u provide me the program for QPSK in Rayleigh fading environment along with error performance..
@SriLalitha: A bunch of BPSK related posts in Rayleigh channel is available at
http://www.dsplog.com/tag/rayleigh
Hope this helps
thanks sir
Hi,
I’ve just gone through some of your tutorials and I really appreciate the work you are doing. I’ve just subscribed to your feed and will appreciate if you could send me the free ebook as well.
Thanks.
@Divine: Emailed you the instructions
Thanks for that…
plz provide me the code for my project which is described as:-
Consider a 16QAM communication system. The information rate is 2 Mb/s and the
carrier frequency is 12 GHz. Assume perfect synchronization.
a) Simulate the system if the channel is AWGN and draw bit error rate of the system
versus Eb/No. Compare the results with what you obtain in theory.
b) Consider (15,11) Hamming code. Apply this code into the above system.
Compare the results with what you obtain in theory.
c) Simulate uncoded system if we have a Doppler Spread due to mobile movement
in the channel. Simulate and draw the bit error rate of the system for maximum
mobile speed 42.3 Km/Hour. No equalizer is used in the system.
d) Apply coding of part (b) into the system of part (c). Simulate the system and
discuss the results.
e) Design an interleaver for the system of part (d) to improve the coded performance
results. Simulate the system.
f) Discuss all the results.
@salman: Good luck with your assignment
Hello krishna,
I am working on the viterbi decoding of the rate1/2 convolution encoder of constraint length 7. I am facing difficulty in coding the state metric and traceback unit of viterbi decoder on matlab as there will be 64 states. could you please help me out in this.
@abc: Please take a look at http://www.dsplog.com/tag/viterbi/
sir i need MMSE equalizer for 16 QAM.
@Anita: Is it a 1tx-1rx system?
Hello Krishna Pillai.
i want help
if we generate random signal to 16qam like this:
x= rand(1,100000);
s=(x<1/16)*(3+3i)+(x1/16)*(3+i) +…….etc
then if we want to know number of error we added noise to this signal
sig=(x>0)*(3+3i) % test one of 16 qam
n=awgn(sig,snr) ;
error=n<2|imag(n)<2;
prob=sum(error)/100000
so that this result should be compatible with theoretical law
but the result is not compatible ,please where is the error
@mohammad: Are you able to get zero errors if you do not add noise?
hi krishna
Simulate & Compare the BER of a 8-PSK system and a 8-QAM system with grey coding and Eb/No==0,2,4,6,8,10 dB
can you plz post the steps to run this program?
thanks,
sunita
@sunita: The post comparing 16PSK and 16QAM might be of help to you
http://www.dsplog.com/2008/03/29/comparing-16psk-vs-16qam-for-symbol-error-rate/
{ 3 trackbacks }