Symbol Error Rate for 16PSK
If you're new here, please click here to SUBSCRIBE and receive for FREE articles over email. Thanks for visiting! Happy learning.
In this post, let us try to derive the symbol error rate for 16-PSK (16-Phase Shift Keying) modulation.
Consider a general M-PSK modulation, where the alphabets,
are used.
(Refer example 5-38 in [DIG-COMM-BARRY-LEE-MESSERSCHMITT]
Figure: 16-PSK constellation plot
Deriving the symbol error rate
Let us the consider the symbol on the real axis, i.e
.
The received symbol .
Where the additive noise follows the Gaussian probability distribution function,
with
and
.
The conditional probability distribution function (PDF) of received symbol given
was transmitted is:
.
As can be seen from the figure above, due to the addition of noise, the transmitted symbol gets spreaded. However, if the received symbol is present with in the boundary defined by the magenta lines, then the symbol will be demodulated correctly.
To derive the symbol error rate, the objective is to find the probability that the phase of the received symbol lies within this boundary defined by the magenta lines i.e. from to
.
For simplifying the derivation, let us make the following assumptions:
(a) The signal to noise ratio, is reasonably high.
For a reasonably high value of , then the real part of the received symbol is not afected by noise i.e.,
and
the imaginary part of the received symbol is equal to noise, i.e.
.
(b) The value of M is reasonably high (typically M >4 suffice)
For a reasonably high value of M, the constellation points are closely spaced. Given so, the distance of the constellation point to the magenta line can be approximated as
.
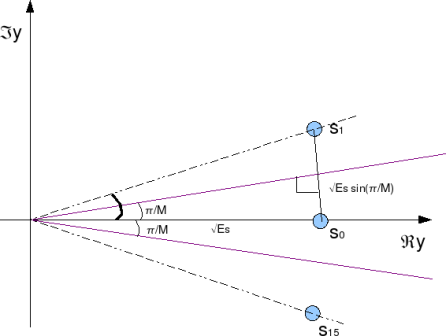
Figure: Distance between constellation points
Given the above two assumptions, it can be observed that the symbol will be decoded incorrectly, if the imaginary component of received symbol
isgreater than
. The probability of
being greater than
is,
.
Changing the variable to ,
.
Note: The complementary error function, .
Similarly, the symbol will be decoded incorrectly, if the imaginary component of received symbol
is less than
. The probability of
being less than
is,
.
The total probability of error given was transmittd is,
.
Total symbol error rate
The symbol will be in error, if atleast one of the symbol gets decoded incorrectly. Hence the total symbol error rate from M-PSK modulation is,
Simulation model
Simple Matlab/Octave script for simulating transmission and recepetion of an M-PSK modulation is attached. It can be observed that the simulated symbol error rate compares well with the theoretical symbol error rate.
Click here to download: Matlab/Octave script for simulating symbol error rate curve for 16 PSK modulation
Figure: Symbol Error rate curve for 16PSK modulation
Hope this helps. KrishnaReferences
[DIG-COMM-BARRY-LEE-MESSERSCHMITT]
(No Ratings Yet)
Loading ...If you liked this post, you may leave a comment below, or subscribe to the RSS feed.
You may also find these posts relevant...
Comments
In your simulation, you have added noise voltage/level i.e taken 20log10(ns) whereas for calculating theoretical BER , you have used noise power. (10log10(ns^2)). I always tend to get confused between these. Do you know any study material clarifying these and some examples?
thanks
mahesh
@mahesh:
Yeah… i agree. it takes a bit of time to get used to 20*log10() or 10*log10() … 
My rule of thumb is as follows:
(a) for voltage signals use 20*log10()
(b) for power signals use 10*log10().
In the code, as you observed,
(a) for scaling noise, which is a voltage signal, I used the 20*log10().
(b) for finding the theoretical symbol error rate, the Es/No in dB (which is signal power by noise power), the conversion used is 10*log10().
Hope this helps.
Regards,
Krishna
Krishna
1. The symbol error rate should also be related to Modulation Error Rate (MER). Since MER is what most Meters measure a correlation will be most helpful.
2. Most of the signal are distributed over a network. What one also needs is the MER impairments due to network elements.
For example if the signal is split into two parts. That splitter will have an insertion loss which will have a spatial component. For example a 2 way lossless splitter will reduce the signal and noise by 3 dB and hence will not impair the signal. However there is an associated resistive loss aboput 1 dB. How much will the MER deteoriate?
Regards
Rajesh Kher
Dear Krishna
Thanks for the reply. While you are right, however we will have to add the noise level. Now the noise level at room temp will be about 3 dBuV while that for QPSK with MER of 15 dB at Signal strength of 86dBuV will be approx 71 dBuV. So that the additive White noise is negligible. We also find that C/N does not get deterioted as we pass thru varios devices.
However we have noticed that MER doe reduce by 0.7-1.0dB.
Question is
1. If thye device contains diodes then if at the point of operation diode is non linear it can add to the reduction of MER but not of C/N. How MER is related to non-linear CSO and CRB.
2. If the device is poorly matched then agian MER measurement will get affected. How does the mismatch between the device and the instruments affects the MER?
Reagards
Rajesh Kher
@Rajesh:
1. If the device is non-linear, one would expect that the signal at the output will have more frequencies than the signal at the input (generation of harmonics dye to x^2, x^3 terms etc).
The out-of-band frequencies maybe filtered out, however nothing much can be done about the harmonics in the in-band. It may be that the measured power includes both out-band and in-band harmonics (along with the desired signal power), hence the C/N does not degrade. However, since the in-band harmonics are not deisrable for demodulation, there is degradation in the MER.
2. When you say ‘devices not matched’, I would think that you are referring to impedence mismatch between the devices (resulting in reflection…). May I suggest the generation of in-band and out-band frequencies due to impedence mismatch as a probable reason for MER degradation.
Does this perspective makes sense? Thanks for these nice questions…
hi i am doing M.E wireless tech. now i am doing my final sem project is implimentation of synchronization algorithem for wimax ieee 802.16e standard.
in wimax ieee802.16e standard
for synchronization purpose they are using preamble .in that preamble they using dc subcarrier .why they are using dc subcarrier… please if any one knows clarify my dought…its urgent
with regards
rajesh neelakandan