In a previous post (here), we discussed in brief, Orthogonal Frequency Division Multiplexing (OFDM) transmission. Let us know probe bit more into the motivation of cyclic prefix (aka guard interval) associated with each OFDM symbol.
What is cyclic prefix?
Let us consider one subcarrier (subcarrier +1 specified in IEEE 802.11a specification) alone. In the figure shown below, the blue line corresponds to the original sinusoidal where one cycle of the sinusoidal is of duration 64 samples ( with 20MHz sampling), corresponding to subcarrier of frequency 312.5kHz.
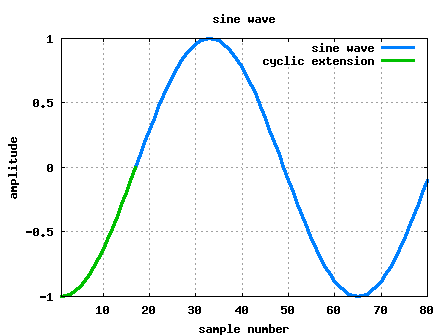
Figure: Sinuosoidal with cyclic prefix
To add the cyclic prefix, 16 samples () from the end of the sinusoidal are appended to the beginning of the sinusoidal (shown in green colour). As can be seen, appending of cyclic prefix does not cause any discontinuities and we still have the original sinusoidal of frequency 312.5kHz.
Further, after adding cyclic prefix, as the sinusoidal is of duration , we now have a bigger window for choosing one period of the sinuosidal. Ofcourse, depending on which set of
is chosen, the phase needs to be corrected, but that will be a trivial operation in a typical implementation.
Effect of passing a sinusoidal through a multipath channel
Let us consider a simple multipath channel of the form
.
Let the transmit symbol be a single sinusoidal .
The received signal is
.
As can be seen from the above equation, after passing through the multipath channel, the received signal is the original sinusoidal albeit with modifications in amplitude and phase.
Use of cyclic prefix in multipath channel
Cyclic prefix acts as a buffer region where delayed information from the previous symbols can get stored. The receiver has to exclude samples from the cyclic prefix which got corrupted by the previous symbol when choosing the samples for an OFDM symbol. Further, from the previous section, we learned that a sinusoidal added with a delayed version of the same sinusoidal does not affect the frequency of the sinusoidal (it only affects the amplitude and phase).
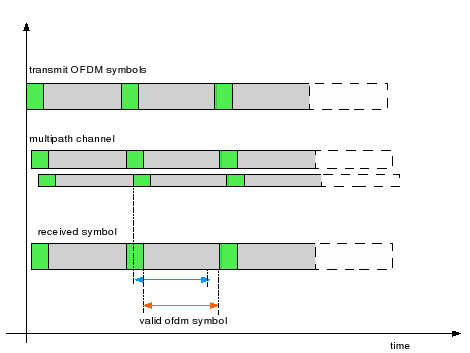
Figure: OFDM symbol with multipath
Given so, for demodulating the received symbol, the receiver can chose samples from a region which is not affected by the previous symbol. As shown in the figure above, the samples can be chosen from the blue-arrow region OR the orange-arrow region OR somewhere inbetween. 🙂
Note:
When the pertinent samples of an OFDM symbol is taken (as explained above), the orthogonality aspect in OFDM is not affected by the multipath channel i.e. eventhough the individual subcarriers undergo phase and amplitude change, as the frequency is not affected, there is no interference between the subcarriers.
Cons of cyclic prefix
Ofcourse, the flipside of adding cyclic prefix is the loss in data rate as we are conveying redundant information.
Choosing the cyclic prefix duration
Given that transmission of cyclic prefix reduces the data rate, the system designers will want to minimize the cyclic prefix duration. Typically, cyclic prefix duration is determined by the expected duration of the multipath channel in the operating environment. For example, for the indoor wireless multipath channel, the typically expected multipath channel is of around duration, hence determining the cyclic prefix chosen per the IEEE 802.11a specification.
Summary
1. Passing a sinsuodial through a multipath channel does not affect the frequency of the sinusoidal.
2. As the multipath channel does not change the frequency of the sinusoidal, multipath channel does not affect orthogonality of the subcarriers (only if the receiver chooses samples which correspond only to the delay-added versions of the samples of the current symbol).
3. Transmission of cyclic prefix reduces the data rate, hence the cyclic prefix duration should not be much more than the duration of the maximum expected multipath channel.
References
[802.11A] Wireless LAN Medium Access Control (MAC) and Physical (PHY) Layer specifications – High speed physical layer in 5GHz band
Hope this helps.
Krishna




Hi Krishna,
I have one doubt regarding the addition cyclic prefix.
I am unable to understand, what will happen to the performance of OFDM based system if I add cyclic prefix at the end (I can’t say prefix now!!!) i.e. copy few sinusoidal carriers from beginning and add at the end of the symbol.
I find this option (called POSTFIX hence onwards) is better than prefix as the sinusoidal will be of lower frequency in POSTFIX and change is phase can be easily estimated than that of PREFIX. What is your opinion.
Also I was thinking that this prefix/postfix gives 2 copies of same data, can we use this redundant information to improve performance.
Thank you.
@Abhijith: Cyclic prefix vs postfix will not have any impact of the sinusoidal frequency. From a quick thought, I do not see any difference in performance between prefix vs postfix.
The point about using the cyclic prefix to improve the performance is worth exploring. In theory, by averaging, we can reduce the impact of noise on duplicated samples (which is a subset of the total symbol) by 3dB. I do not know how much this translates to improving the per-tone SNR.
Hi Krishna, thanks for your work!! I understand that cyclic prefix is nothing but adding the last bit of the symbol to the front.
But, why do we copy the last bit of subcarriers to the front? How does this going to copy the last bit of symbol to the front?? Should we perform cyclic prefix before or after parallel to serial conversion??
Please advice. Thank you again!
@Me: It is appending of last few samples of the time domain samples (after ifft) to the front.
Thanks very much Krisha, it makes sense now! Cheers!
Hi Krishna, excellent work there. I would like to find out a very detailed information, after performing IFFT, we should add CP before parallel to serial conversion or after?
Another important information, your matlab code in:
http://images.dsplog.com/db-install/wp-content/uploads/2008/08/script_ber_bpsk_ofdm_rayleigh_channel.m
You never performed parallel serial until after channel convolution, but that is not the real case in real world implementation right? You suppose to convert to serial stream and only then convolute with the channel, please advice.
Thanks very much.
@Mar:
In the code, each ofdm symbol is getting convolved with a different channel realization.
What is the overhead of the cyclic prefix? How do I calculate it and how does it effect the system data rate?
@Sarath: Hmm.. let me explain by pluggin in some number from 802.11a wlan as an example.
For 6mbps case, we have 24 bits being send in a 4us symbol (of which 0.8us is the cyclic prefix, and 3.2us is the symbol duration). If we make the cyclic prefix smaller to 0.4us, then 24bits goes in a 3.6us symbol (=3.2+0.4). The data rate becomes 6.6667us
I have one doubt. At the receiver we take only the symbol which does not suffer from interference from the previous symbol. But that symbol has indeed suffered from the interference from the same symbol. Will that not affect the decoding?
@Venkatraman: A sine wave added with a delayed version of itself is still the same sine wave (no change in frequency), but affects only the amplitude and phase i.e. there is no loss in orthogonality. The change in amplitude and phase can be corrected by a channel estimation block
Nice explanation. I found your blog only today. I wish I had seen this before.
Keep up the work.
Thank you.
Hi krishna,
You are doing a wonderful job. Stay blessed!
hii…
can u tell me how to add the cyclic prefix in matlab coding…as i know what is cylic prefix…bt i m nt getting the idea that how to copy the last 16 symbols before the 64 carriers…
pleaseeee help me with the codes..
@shraddha: Should be reasonably straightforward. For eg, if
x = [1 2 3 4 5 6 7 8]; and if you wish to copy the last to samples to the first
x_wth_cp = [x(7:8) x];
helps?
what is the meaning of physical layer implementation based on 802.11g using ofdm?
@arun: You might have heard about the OSI model having seven layers. The layers are used to characterize different logical blocks in a communication link.
http://en.wikipedia.org/wiki/OSI_model
Physical layer is the one which pushes the bits over wired, wireless etc.
http://en.wikipedia.org/wiki/Physical_layer
can anyone explain the concept of estimation of frequency offset in awgn channel using ofdm technique by use of cyclic extension, guard interval, pilot insertion and etc
@srikant: The frequency offset estimation on 802.11a short preamble using autocorrelation is discussed at
https://dsplog.com/2008/03/03/frequency-offset-estimation-using-80211a-short-preamble/
it is very good for me.this site is very good for me and i will use it.
hi
can u say me how to add a delay to the signal.
later adding a factor say a factor of 0.2 to it
@uday: In Matlab, if you have a vector x = [1 2 3 4 ], then delay can be notionally added by x_delay = [0 0 0 x]; Helps?
Very useful site and ur explanations are realy good and helpfull. I’m quite new when using Matlab, but able to understand script when reading :). Therefore, I need your help and guidance because I want
a) to graphically display the output signal from the transmitter, before the entrance to the channel, that I’m able to show degradation of the signal before and after tha chanell,
b) also I would like to show the figure of the signal before and after adding a cyclic prefix,
c) If there is a possibility to show the result of BER in matrix form in a way that is seen quantity if errors.
I hope that you would be able to help by providing me the missing peace of code/script so that I can continue my work . In advance grateful.
@anesa: You can add plot() commands at each stage.
Hi..
I have a question. Assume rect pulse shaping.
When looking at the OFDM signal in the frequency domain, will the nulls of the sinc for each subcarrier still pass through the peaks of other subcarriers even after the addition of cyclic prefix? I doubt this because 1/(OFDM symbol duration) ~= subcarrier spacing. Subcarrier spacing = 1/(OFDM Symb time-guard time).
If this is the case wont the subcarriers interfere? I am able to visualize the orthogonality in the time domain even after addition of CP by your explanations. But when the cyclic prefix is added it seems as if orthogonality is lost in the “freq domain” since the nulls don’t pass through the peaks of other subcarriers anymore. The PASSBAND BW for each subcarrier seems to have reduced to 2/Tofdm instead of 2/(Tofdm -Guard Time)
Would be gr8 if you can provide an expln.
Thanks,
Nachi
@Nachi: Adding cyclic prefix does not affect the orthogonality. Having cyclic prefix gives us the flexibility to take OFDM symbol duration worth of samples from anywhere in the OFDM symbol.
I think i got your question;
Actually adding cp will not make any problem for the orthogonality, cause, cp is adding with the original sinusoidal wave in each of the subcarrier which leads to the orthogonality again with zero ISI and no frequency changing, that is the flexibility replied Mr. Krishna . so that now we can get the original signal at the receiver by taking any symbol duration……
Thank you. hope it will help to visualize.
The Cyclic Prefix(Cp) should be greater than the maximum delay spread(mds). So is there any specific mathematical equation or relationship between CP and mds??Please reply
@Budhaditya: Well, if we want to prevent Inter Symbol Interference, the CP should be longer than the delay spread.
Thanks Krishna for the reply. However could you provide any help regarding the relationship between Channel SNR and Cyclic Prefix. I mean to say is there any standard theory behind the selection of CP with respect to SNR.?? Pls rply
@Budhaditya : I do not think that the SNR and CP are related. Why do you think so?
Thx ur nice work!I like your website very much!
Hi,
In this article you said’…eventhough the individual subcarriers undergo phase and amplitude change, as the frequency is not affected, there is no interference between the subcarriers.’
a) Do you mean the orthogonality between differenet subcarriers will be kept?
b) And is it because all the other subcarriers in the same signal undergo the same amout change in phase?
If my opinion is not correct,then how does it works in detail?
Thanks for your help!
Eric
@Eric Cheung: MY replies
a) Yes. No interference between the subcarriers
b) No. Each subcarrier can undergo a different phase and amplitude change.
The logic is that : if sin(wt) and sin(2wt) are orthogonal, then Asin(wt) and Bsin(wt+phi) is also orthogonal.
is there should be Bsin(2wt+phi)?
@Michael: where?
I’m working on ofdm.very useful website.thanks
@lakshmi: Thanks
dear sir,
i’m working on UWB -MB-OFDM .can u plz help me giving any channel estimation code used in both multi band and single band.
@BIKRAMADITYA DAS: Well, I do not have any codes for channel estimation. But I would guess, it would be some thing like
– send a known transmit sequence x
– assume the channel is h
– the received signal y = hx+n
– as x is known at the receiver, the estimate of h is = y/x = h + n/x
pls do you have the matlab code show the effect of the cyclic prefix in the ofdm system .pls advaise me
@bakkar: Please look at the post on BER for BPSK in OFDM with Rayleigh multipath channel.
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
In that you can see that though there is multipath, there is no intersymbol interference, thanks to the cyclic prefix.
Hi
I have a little doubt about correct position of fft window. In different articles and papers it is mentioned that fft window should be aligned with the strongest multipath signal.
You have aligned it with your first multipath component in the above figure. What if strongest multipath components are delayed relative to the first arriving paths.
In other words suppose this is my channel impulse response
h=[0.1 1 0.2 0 0.3]
How can I extract the info using the signal delayed by one sample. Because first copy of signal is difficult to be found at the reciever due to noise and synchronization issues.
@jenna: Well, as long as the multipath does not cause ISI, its best to collect all the copies of the received signal.
If for some reason, you dont want to pickup the pre-cursor taps, its also fine. Just make sure that the channel estimation is also done on the preamble which is extracted in the same way. That will take care of the phase rotation due to the channel.
what is the advantage of cyclic prefix, over zero padding?
@srikanth: I have not studied the topic, but a quick googlig gave me the paper
Cyclic Prefixing or Zero Padding for Wireless Multicarrier Transmissions? – Bertrand Muquet, Zhengdao Wang, Georgios B. Giannakis,
Marc de Courville and Pierre Duhamel, IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 50, NO. 12, DECEMBER 2002
Some key points:
1) the presence of zeros between the symbols ensure that there is no inter symbol interference. Hence channel becoming 0 is less likely and we are better off.
2) I think the receiver equalization is bit more complex, but did not understand that aspect well.
I would urge you to refer to the above paper for further details.
very useful site and ur explanations are realy good.Iam working on an project in mimo ofdm i want to design an ofdm and use mimo in it . i would be thankful if u could help me.thanking u in advance.
@sowmia: Sure, please ask questions. I will answer to the best of my knowledge
hello…
we didn get the exact meaning of cyclic prefix..hw can i implement it in ofdm channel.if possible can u plz provide us the code.
@sona: Cylcic prefix is inserted by just copy pasting last N samples of a symbol to the beginning of the symbol. The post simulating BER with OFDM in Rayleigh multipath channel discuss insertion of cyclic prefix. Please refer
https://dsplog.com/2008/08/26/ofdm-rayleigh-channel-ber-bpsk/
Hope this helps.
Hello Krishna, thanks for ur nice work on OFDM.
I have run ur simulation of ofdm in rayleigh multipath channel with and without cyclic prefix. But I dont get any difference in the result.why? where actually this thing work?
How can I use the doppler shift in the rayleigh simulation?
is there any problem if we use the Matlab build-in function chan = rayleighchan(ts,fd) as channel estimation?
@Masum: My replies:
1. Its surprising that you were able to obtain similiar performance with and without cyclic prefix in a multipath channel. How many taps were your channel. And what was your cyclic prefix duration?
2. Sorry, I have not tried modeling doppler.
3. I have not used rayleighchan() function. Hence unable to comment.
@ venkatesh:
May I point you to a nice article on CommsDesign from Anuj Batra et al (Texas Instruments).
URI: http://tinyurl.com/yvfvu3
As explained in the artcle, in multband OFDM, the transmission of an OFDM symbol of bandwidth 500MHz is performed on three channels (with the transmissions seperated in time).
To enable the transmitter (and receiver) to switch channels there is small gap of 9.5ns (called as guard interval) where there is no information transmitted.
Further, as in typical ofdm implementations, there is a cylcically rotated version of each ofdm symbol appended to tbe beginning of the symbol (called as cylcic prefix). Ref: Fig2.
The chosen value of cylcic prefix should ideally be longer than maximum expected channel delay (to avoid inter symbol interference). However, long cyclic prefix implies a loss in data rate. Based on simulations, cylcic prefix duration of 60.6ns is chosen. (Ref: Fig4)
Hope this helps. Kindly revert for clarifications.
we want the apt meaning of cyclic prefix in multiband OFDM