In a previous post (here), we looked at using CORDIC (Co-ordinate Rotation by DIgital Computer) for understanding how a complex number can be rotated by an angle
without using actual multipliers. Let us know try to understand how we can use CORDIC for finding the phase and magnitude of a complex number.
Basics
The CORDIC algorithm is built on successively multiplying the complex number , by
. As can be noticed, as the elements of
can be represented in powers of 2, the multiplication can be achieved by using the appropriate ‘bit shift’. For further details, please refer to the previous post (CORDIC for phase rotation).
Finding the magnitude and phase
It is reasonably obvious that the multiplying a complex number by
does not change the magnitude of
.
Given so, if phase rotation of results in
, and the imaginary component of
is 0, then the real part of
stores the magnitude of
.
To put in equations, if
, where
,
then,
(real part of
is the magnitude of
)
(the rotation angle
is the negative of the phase of
)
This is the fundamental idea behind finding the magnitude and phase of a complex number using CORDIC.
The sequence of events is as shown below:
(a) The input complex number is subject to a series of phase rotations.
(b) The sign of the phase rotation is the negative of the sign of imaginary component of .
(c) After multiple iterations, imaginary component of tends to zero.
(d) Then, the real part of the new complex vector represents the magnitude and the cumulative phase value represents the negative of the phase of .
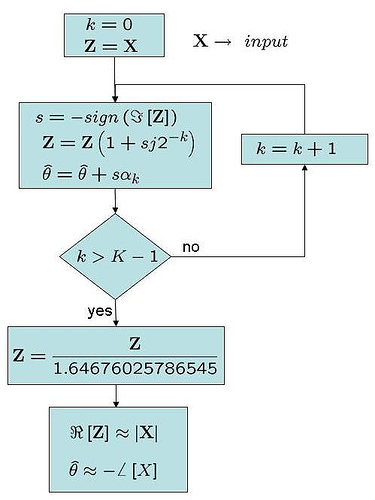
Figure: Flow chart for the operations involved in using CORDIC for computing phase and magnitude
The reference phase (phase of
).
The scaling factor of 1.64676025786545 is to remove the ‘gain’ following successive rotations by . Please look at the previous post on CORDIC (here) for details.
Note:
If the input complex number lies in the second or third quadrant, it needs to be first shifted to the first/fourth quadrant before we start the sequence of events shown in the figure above (as the CORDIC range is limited to around +/-90 degrees). This can be achieved by multiplication by or
, as appropriate.
Simulation model
Simple Matlab/Octave script for computing the phase and magnitude of a complex number using the CORDIC approach. Quick comparison indicate that the computed and acutal values are closely matching.
Click here to dowload
Reference
[DSPGURU-CORDIC] CORDIC FAQ in dspGuru(TM)
Hope this helps.
Krishna