Question 38 on Communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.
Q38. A binary symmetric channel (BSC) has a transition probability of 1/8. If the binary transmit symbol X is such that P(X=0)=9/10, then the probability of error for an optimum receiver will be
(A) 7/80
(B) 63/80
(C) 9/10
(D) 1/10

Solution
The solution to the problem seem deceptively reasonably simple. Quoting from the Wiki entry on Binary Symmetric Channel
A binary symmetric channel (or BSC) is a common communications channel model used in coding theory and information theory. In this model, a transmitter wishes to send a bit (a zero or a one), and the receiver receives a bit. It is assumed that the bit is usually transmitted correctly, but that it will be “flipped” with a small probability (the “crossover probability”). This channel is used frequently in information theory because it is one of the simplest channels to analyze.”
In our example, the transition probability i.e probability of transition (i.e. 1 becoming 0 or 0 becoming 1) for each alphabet is given as 1/8. probability of correct transmission, for each alphabet is given as 1/8 (the probability of incorrect transition is 7/8).
The transition probability diagram with the above data can be drawn as,
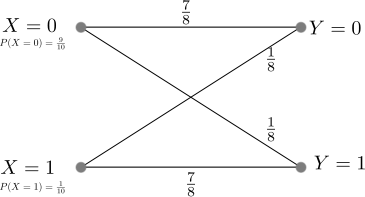
Figure : Transition probability diagram for a binary symmetric channel
The probability of the source alphabets are,
.
The transition probability when is :
.
Similarly the transition probability when is :
.
The received alphabet not equal to the transmitted alphabet is,
.
Hold on, we are not done yet.
Update (9th Nov 2012):
The above gives the probability that the received symbol is not equal to the transmitted symbol, and not the probability of error for an optimum detector. Thanks to Mr. Raghava GD who rightly pointed out in the comment section that – “the calculation that you did just gives the probability of receiving the bit erroneously and it doesn’t tell anything about the probability of error for an optimum decoder.”
After digesting his comments, and referring from Section of 1.2 of Chapter 1 of Prof. John M. Cioffi’s book ,
Consider the channel model which produces a discrete vector output for a discrete vector input. The detector chooses a message from all possible messages
transmit vectors. The channel input vector
results in a corresponding channel output vector
. The decision device translates the received vector
to an estimate of the transmitted vector
and a decoder converts
to the estimate of the message vector
.

Figure : Vector channel model (Reference : Figure 1.13 in Chapter 1 of Prof. John M. Cioffi’s book)
The probability of error is defined as,
.
Correspondingly, the probability of being correct is,
.
The optimum detector chooses to minimize the probability of error
or equivalently maximize
.
The probability of making the correct decision , given the received vector
is
.
The above quantity known as the posteriori probability, and an optimum decision device will try to maximize the above quantity. The Maximum a Posteriori Detector (MAP), is defined as the detector that chooses the index to maximize the a posterior probability
given the received vector
.
Using Bayes therorem, the posterior probability can be written in terms of prior probability and the channel transition probability
,
.
Note :
The term is a constant and can be ignored when trying to maximize the posterior probability
.
The MAP detection rule is,
.
Note :
This is discussed briefly in Chapter 5.1.3 The Optimum Detector in Digital Communications, Fourth edition John G. Proakis (buy from Amazon.com, buy from Flipkart.com)
Applying the MAP detection rule to the problem at hand :
We have two candidates 0 and 1 for the source message i.e
a) ,
b) modulator is a pass through i.e and
c) received symbol can be 0 or 1.
The goal is to make decision rule on the observed received symbol .
Applying MAP detection rule,
.
.
In both the cases i.e when received symbol , the optimum MAP detection rule suggest that the estimated message symbol is
.
Intuitively, this makes sense : given that , a receiver will be better of assuming that the transmitted symbol is always 0. With this, the probability of making an error in the decision is
.
Matlab example
clear all; close all; % number of observations N = 10^5; % generating x with p(x=0) = 9/10, p(x=1) = 1/10 x = (rand(1,N) > 9/10); % generating c with p(c=0) = 1/8, p(c=1) = 7/8 c = (rand(1,N) < 7/8); % binary symmetric channel y = mod(x+c,2); xhat = 0; % counting errors nErr = size(find(xhat-x),2); errProb = nErr/N
Based on the above, the right choice is (D) 1/10.
References
[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf
[2] Wiki entry on Binary Symmetric Channel http://en.wikipedia.org/wiki/Binary_symmetric_channel
[3] Chapter 1 of Prof. John M. Cioffi’s book
[4] Wiki entry on posteriori probability
[5] Wiki entry on Bayes therorem
[6] Digital Communications, Fourth edition John G. Proakis (buy from Amazon.com, buy from Flipkart.com)




For some combination of probabilities P(X=0) and the transition probabilities, would there exist a situation where the MAP decoder’s decision would dependent on Y. In such a case, what would be the error probability in decoding?
Eg: P(X=0) = 0.9 and transition probability = 0.91
What would be the MAP decoding error probability in this case?
Such cases can be formed from the following two sets of inequalities:
1. Pt 1
2. Pt < P(X=0) and Pt + P(X=0) < 1
Here, Pt stands for transition probability for a BSC.
@Pravin: I believe that was a comment rather than a question. I reckon, the MAP detector rule described above should hold good in that case too. Yes, the decision rule will be based on the transition probabilities and input probabilities
Sorry for the typo in my previous comment “receiver can decide to decode to 0 irrespective of ‘Y’”.
@Raghava: Hmm… I can appreciate the rationale – biasing the hypothesis to minimize the probability of error in Gaussian channel conditions. How does that work for binary symmetric channels?
Can you please share your opinion
Ok,
I will try to prove it analytically here.
Before, i need to clarify that the “transition probability = cross-over probability = 7/8”. Cross-over probability is also called transition error probability or transition probability. In fact if you don’t agree with the definition you can still go ahead, by flipping the received values, and considering this flipping of bits as part of the channel, which changes the BSC to a BSC with crossover probability 7/8. Lets call this, “modified BSC” and all the further calculations are for this “modified BSC”.
In fact you can prove that this modification does not change the optimality of the receiver. If you are not convinced i can give you the proof.
The optimum decoder at the receiver should do maximum likelihood decoding.
So according to ML rule, if the received value is 1 then the decoder should decide X = 0, if the ratio Pr( X = 0 | Y = 1 ) | Pr( X = 1 | Y = 1 ) is greater than 1, X = 1 otherwise.
The ratio
Pr( X = 0 | Y = 1 ) | Pr( X = 1 | Y = 1 ) = Pr( Y = 1 | X = 0 ) *Pr(X = 0 ) |
Pr( Y = 1 | X = 1 ) * Pr(X = 1)
= 1/8 * 9/10 | 7/8 * 1/10
= 9/7 > 1.
So the receiver should decode to X = 0 if Y = 1 is received.
Similarly if the received value is 0 then the decoder should decide X = 0, if the ratio Pr( X = 0 | Y = 0 ) | Pr( X = 1 | Y = 0 ) is greater than 1, X = 1 otherwise.
The ratio
Pr( X = 0 | Y = 0 ) | Pr( X = 1 | Y = 0 ) = Pr( Y = 0 | X = 0 ) *Pr(X = 0 ) |
Pr( Y = 0 | X = 1 ) * Pr(X = 1)
= 7/8 * 9/10 | 1/8 * 1/10
= 63 > 1.
which tells me that the receiver should decode to X = 0 even if Y = 1 is received. i.e irrespective of Y, optimum decoder should decode to X = 0
Let X be the transmitted bit and X’ be the bit to which the receiver decodes to.
So the probability of error Pr( error)
= Pr( X’ != 0 | X = 0 ) Pr ( X = 0)+ Pr( X’! = 1 | X = 1 ) Pr ( X = 1)
= 0 * 9/10 + 1 * 1/10.
= 1/10
Sorry again for the typo:
” In fact if you don’t agree with the definition you can still go ahead, by flipping the received values, and considering this flipping of bits as part of the channel, which changes the BSC to a BSC with crossover probability 1/8 “
And the calculation that you did just gives the probability of receiving the bit erroneously and it doesn’t tell anything about the probability of error for an optimum decoder.
ps: sorry for multiple comments 🙂
@Raghava: Thanks for the detailed comments – am yet to digest with all the gory details. However, can appreciate that if P(X=0)=9/10, then we are better off ignoring Y and assuming that Y=0 always –> translating to probability of error of 1/10.
Like I did for the post on Gated SR Latch, will do an Update on this post once am ready. Thanks for helping to make the contents of the blog better. Appreciate it! 🙂
@Raghava: I updated the answer with explanations using the Maximum A Posteriori (MAP) Detection rule
https://dsplog.com/2012/11/03/gate-2012-ece-q38-communication/#update
Please do share any comments, if needed.
No comments!! 🙂 .. i had an other typo which i realized after seeing the update..I should have written MAP rule instead of ML rule for an optimized decoder.
Thanks 🙂
@Raghava: Thanks. Yes, I recall seeing that – but the point is that the required message was conveyed without error 😉
Answer is 1/10 which is D. The crude reasoning that i can give is, since the most of the times transmitter is transmitting 0 the receiver can decide to decode to 1 irrespective of ‘Y’, then the probability of error is probability of transmitting 1 which is 1/10. So the answer is D.
Now to prove it optimum needs some analytical reasoning which i will post in other comment if needed.