In the post on Viterbi decoder and soft input Viterbi decoder, we discussed a convolutional encoding scheme with rate 1/2, constraint length and having generator polynomial
and having generator polynomial
. If the number of uncoded bits is
, then the number of coded bits at the output of the convolutional encoder is
. Decoding the convolutionaly encoded bits by Viterbi algorithm consisted of the following steps.
1. For group of two bits, compute Hamming distance or Euclidean distance (for hard decision or soft decision respectively)
2. For each of the states, compute the path metric knowing the following.
- Each state can be reached from only two previous states (out of the 4 possible states).
- For each possible transition, compute the branch metric by adding the path metric of the previous state to the Hamming/Euclidean distance of the transition
- Select the branch metric which is minimum among the two values and store it as the path metric for the current state
3. Store the survivor predecessor state for each state.
4. Once we have processed received bits, we know that the convolution encoder has reached state 00. We start traceback from state 00, and given that we know the current and previous state, the
input bits can be decoded.
However, when the number of input uncoded bits is large, the memory requirements for a survivor state matrix of dimension
becomes impossible to manage.
Traceback with finite survivor memory
To be able to decode with finite survivor memory, lets say we need to start the traceback at some time instant , where
is the decoding depth and
is the traceback depth.
The sequence of events are as follows:
- At time instant
, we start the traceback and continue tracing back through the survivor path
times. Once we are done with the traceback, we start estimating the
decoded bits knowing the current state and previous state.
- Similarly, we again start the traceback at time
, do traceback
times and then decode bits from
to
.
- Once we reach the end of the input sequence at time instance
, we know that trellis has converged to state00 and then we do demodulation with traceback.
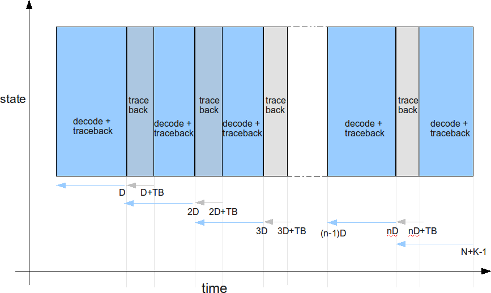
Figure: Viterbi traceback with finite survivor memory
Given that traceback speed is equal to storing the speed incoming coded bits, we can implement the above algorithm with a memory of .
Note: The literature of different architectures for survivor state management is vast and is not explored in this post.
Selecting start state for traceback
At time instant , there are multiple ways to select the state to
- Always start from a defined state (for example state 00)
- Start from the state which has the minimum path metric
From simulations, can identify the minimum value of traceback depth (), which results in performance comparable to infinite survivor path memory case. From simulations shown in the post on hard decision Viterbi decoder, we know that at
, results in a bit error rate of
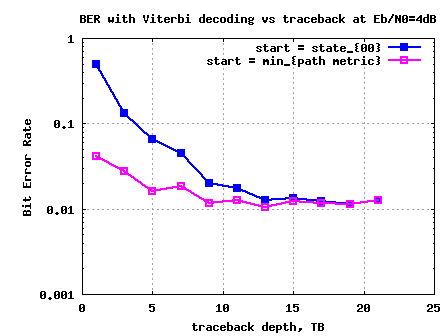
Figure: BER vs traceback depth at Eb/N0 = 4dB
From simulations it has been observed that doing traceback depth of around 15 ensures that the obtained BER with finite survivor state memory is close to the BER with infinite survivor state memory. Note that corresponds to around 5 times the constraint length of
.
Additionally, as expected starting traceback with from the state with minimum pathmetric shows better performance than always starting at state 00.
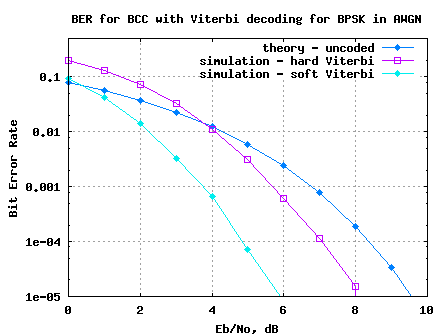
Simulation results
Click here to download Matlab/Octave script for simulating bit error rate vs traceback for Eb/N0 = 4dB.
Click here to download Matlab/Octave script for simulating BER for BPSK with convolotional coding with hard/soft decision Viterbi decoding and with finite survivor state memory
Warning: This simulation took around 10hrs to complete. Am thinking that I will move to C code for simulations involving lots of for-loops.
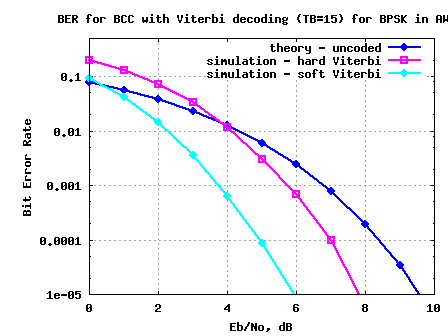
Figure: BER for BPSK with convolutional coding with finite survivor state memory
Reference
Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt




in this communication very interest,,,,,,,,
Mr. Krishna:
Because I’m trying to understand these math equations and describe in this
article, so I confused why some equations can’t display.
thanks~
@Wig: I checked the post. From a quick look, I see that all the equations are displayed. Am I missing something?
@Wig, @Krishna, some of the math type images are from URIs such as https://dsplog.com/2009/07/cgi-bin/mimetex.cgi?D+2TB which should link to https://dsplog.com/cgi-bin/mimetex.cgi?D+2TB.
@Bill Cassidy: Yes, thanks. I have fixed the errors.
Hello Mr. Krishna
Why some equations can’t display??
https://dsplog.com/2009/07/cgi-bin/mimetex.cgi?D+2TB
https://dsplog.com/2009/07/cgi-bin/mimetex.cgi?\frac{E_b}{N_0}=4\mbox{dB}
https://dsplog.com/2009/07/cgi-bin/mimetex.cgi?10^{-2}
etc.
best regard! Wig
@Wig: Well, remove ‘2009/07’ from the urls. But, why are you trying this?
hi
i have tried this viterbi decoding with finite survivor state memory.but it is giving error at function conv() at the starting of program it self.
can u please help me how to overcome thos problem. i had run this program on matlab 7.6a version.
@rajesh: Can you please copy-paste the error message. This code is working fine on my desktop (in Octave 3.0.1).